IV. Формирование умений и навыков.

Иррациональные числа

П о с т а н о в к а проблемной задачи: как измерить диагональ квадрата со стороной 1.

Можно обратиться к истории этого вопроса.

Математики Древней Греции более двадцати веков тому назад пришли к выводу, что нет ни целого, ни дробного числа, выражающего диагональ квадрата со стороной 1. Это вызвало кризис в математической науке: диагональ у квадрата есть, а длины у неё нет!

Математики нашли выход из этой ситуации: раз имеющегося запаса чисел – целых и дробных – не хватает для выражения длин отрезков, значит, нужны какие-то новые числа. Так появились иррациональные числа.

3. В в е д е н и е множества действительных чисел.

J – множество иррациональных чисел R – множество действительных чисел

4. С р а в н е н и е иррациональных чисел.

Привести различные примеры иррациональных чисел и показать, как они сравниваются.

Вопрос о действиях с иррациональными числами целесообразно рассмотреть на следующем уроке.

IV. Формирование умений и навыков.

1. Даны числа:

9; 0; – 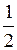; –6(3); 7,020020002…; 1,24(53); 345; π; –7 .

а) Разделить их на две группы: рациональные и иррациональные.

б) Заполнить таблицу:

Натуральные числа	Целые числа	Рациональные числа	Иррациональные числа

Примеры №1 посчитать обязательно.

Верные утверждения выписать