- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ
| §2.10. Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона). | |
| Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул. | |
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.
Мы знаем, что 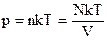 . Следовательно, . Следовательно, 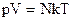 . Учитывая, что . Учитывая, что 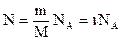 , получим: , получим:  . .
| |
Произведение постоянных величин есть величина постоянная, следовательно: 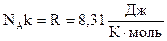 - универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая). - универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
| 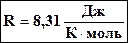
|
Таким образом, имеем:
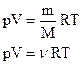 - уравнение состояния (уравнение Менделеева – Клапейрона). - уравнение состояния (уравнение Менделеева – Клапейрона).
| 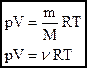
|
| Другие формы записи уравнения состояния идеального газа. | |
1. Уравнение для 1 моля вещества.
Если n=1 моль, то, обозначив объем одного моля Vм, получим:  .
Для нормальных условий получим: .
Для нормальных условий получим:
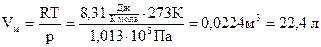
| 
|
2. Запись уравнения через плотность: 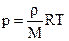 - плотность зависит от температуры и давления! - плотность зависит от температуры и давления!
| 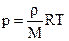
|
3. Уравнение Клапейрона.
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда: 
| |
Эта запись означает, что для данной массы данного газа справедливо равенство: 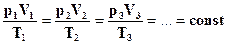
| |
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: 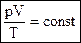 . .
| 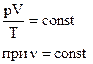
|
| §2.11. Газовые законы. | |
| 1. Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn; p1=p2=…=pn; T1=T2=…=Tn | |
Доказательство:  Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
| |
2. Закон Дальтона.
Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.
Доказать: p=p1+p2+…+pn
Доказательство: 
| |
| 3. Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения. | |
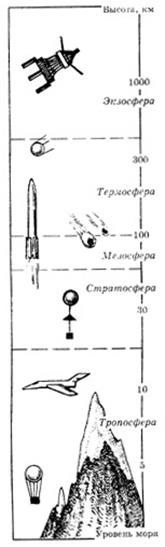
§2.12. Атмосферное давление.
Атмосфера - слой воздуха, который окружает нашу планету. Она представляет собой смесь газов. Атмосфера удерживается притяжением Земли. На нее действует сила тяжести.
Исследования показали, что плотность атмосферы на разных высотах от поверхности Земли различна: она увеличивается по мере приближения к поверхности Земли.
Если последовательно выделять разные уровни, то можно показать, что каждый вышележащий слой атмосферы вследствие притяжения Земли давит на слой, лежащий ниже. Но газы, согласно закону Паскаля, передают производимое на них давление без изменения во все точки. Значит, на разных расстояниях от поверхности Земли состояние атмосферы можно характеризовать своим давлением. Самое большое давление будет наблюдаться вблизи поверхности Земли.
Атмосфера давит на поверхность Земли. Это действие называют атмосферным давлением.Атмосферное давление действует на все тела, находящиеся в атмосфере.
Впервые установил существование атмосферного давления, изобрел прибор для измерения атмосферного давления и измерил его ученик Галилея Эванджелиста Торричелли.
Его опыт состоял в следующем. Узкую трубку длиной 1 м, запаянную с одного конца, Торричелли заполнил ртутью. Закрыв отверстие пальце, он перевернул ее и погрузил в чашку с ртутью. Когда Торричелли отпустил палец, часть ртути вылилась из трубки в чашку. Высота столбика оставшейся ртути в трубке оказалась равной примерно 76 см.
Это явление можно объяснить, если предположить, что давление образовавшегося столба ртути уравновешивает давление атмосферы на уровне свободной поверхности ртути в чашке.
Поместив рядом с трубкой шкалу, Торричелли наблюдал изменение высоты столба ртути в трубке в связи с изменениями в атмосфере и измерял атмосферное давление в единицах "высоты ртутного столба". Этот прибор называется ртутным барометром. За величину нормального атмосферного давления, измеренного таким способом, принято давление столба ртути высотой 760 мм.
В единицах СИ 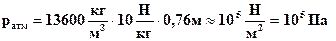 .
Соответственно 1 мм ртутного столба » 133,(3) Па.
Если использовать жидкостные приборы, то давления разреженных газов удобнее измерять в единицах "высоты водяного столба", поскольку плотность ртути в 13,6 раза больше плотности воды. .
Соответственно 1 мм ртутного столба » 133,(3) Па.
Если использовать жидкостные приборы, то давления разреженных газов удобнее измерять в единицах "высоты водяного столба", поскольку плотность ртути в 13,6 раза больше плотности воды.
| 

|
§2.13. ПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ
| Название | Постоянные величины | Зависимость между другими параметрами | Направление процесса |
Графики | Истолкование процесса на основе МКТ
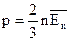
| Скорость протекания | ||
|
| T=const M=const m=const изотермический процесс | 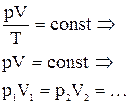
| Изотермическое расширение | p V | V T | p T | VÞ n¯
T=const Þ 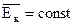 Тогда p ¯ во столько же раз, во сколько уменьшается n, а значит, увеличивается V
Тогда p ¯ во столько же раз, во сколько уменьшается n, а значит, увеличивается V
| Медленно, t>tрелаксации |
| Словесная формулировка | Изотермическое сжатие | p
V | V
T | p
T | V¯Þ n T=const Þ Тогда p во столько же раз, во сколько увеличивается n, а значит, уменьшается V | Медленно, t>tрелаксации | ||
| Для данной массы данного газа при постоянной температуре произведение давления на объем есть величина постоянная (давление обратно пропорционально объему). | ||||||||
|
|
p=const M=const m=const изобарный процесс | 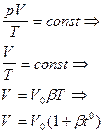 b=1/273 К-1
b=1/273 К-1
| Изобарное расширение (нагревание) | p V | V T | p T | T Þ 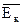
Т.к. p=const, то n¯, следовательно V во столько же раз.
Т.к. p=const, то n¯, следовательно V во столько же раз.
| Медленно, t>>tрелаксации |
| Словесная формулировка | Изобарное сжатие (охлаждение) | p
V | V
T | p
T | T¯ Þ Т.к. p=const, то n, следовательно V¯ во столько же раз. | Медленно, t>>tрелаксации | ||
| Для данной массы данного газа при постоянном давлении отношение объема к абсолютной температуре есть величина постоянная (объем прямо пропорционален температуре). | ||||||||
|
|
V=const M=const m=const изохорный процесс |  a=1/273 К-1
a=1/273 К-1
| Изохорное нагревание | p V | V T | p T | T Þ 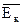
Т.к. V=const, то n=const, следовательно p во столько же раз, во сколько увеличилась температура.
Т.к. V=const, то n=const, следовательно p во столько же раз, во сколько увеличилась температура.
| Медленно, t>>tрелаксации |
| Словесная формулировка | Изохорное охлаждение | p
V | V
T | p
T
| T¯ Þ Т.к. V=const, то n=const, следовательно p¯ во столько же раз, во сколько увеличилась температура. | Медленно, t>>tрелаксации | ||
| Для данной массы данного газа при постоянном объеме отношение давления к абсолютной температуре есть величина постоянная (давление прямо пропорционально температуре). | ||||||||
|
Адиабатный процесс | M=const m=const | 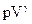 =const
S= const
(изоэнтропийный процесс) =const
S= const
(изоэнтропийный процесс)
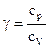
| Адиабатное расширение | P V | V Þ n ¯,т.к. расширение происходит быстро, то p ¯ больше, чем n. Þ T¯ (адиабата круче изотермы) | Быстро по сравнению с изотермическим, но t<tнеобходимого для теплообмена | ||
| M=const m=const | 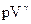 =const
S= const
(изоэнтропийный процесс) =const
S= const
(изоэнтропийный процесс)
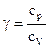
| Адиабатное сжатие | P V | V¯ Þ n ,т.к. сжатие происходит быстро, то p больше, чем n. Þ T (адиабата круче изотермы) | Быстро по сравнению с изотермическим, но t<tнеобходимого для теплообмена | |||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
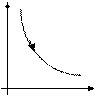
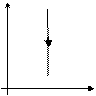
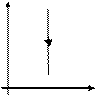
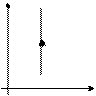
 Закон Бойля-Мариотта
Закон Бойля-Мариотта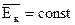
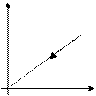 Закон Гей-Люссака
Закон Гей-Люссака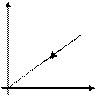
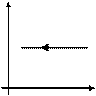
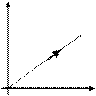
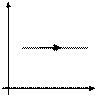

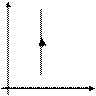 Закон Шарля
Закон Шарля