
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Министерство образования и науки Российской Федерации
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра автоматизации производственных процессов и производств
Расчетно-графическая работа
по курсу:
"Обработка результатов измерений".
Вариант
Выполнил: студент гр. АГ-08-01
Принял: Э.А. Шаловников
Уфа 2011
Обработка выборки.
Таблица 1
Результаты измерений
| |||||||||||||
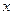
| 1.07 | 0.99 | 1.25 | 0.89 | 1.04 | 1.13 | 0.96 | 1.03 | 1.45 | 1.04 | 1.05 | 0.88 | 1.03 |
| 0.97 | 1.15 | 1.09 | 0.89 | 1.08 | 1.07 | 0.97 |
1. Ранжируем статистический ряд
Таблица 2
Ранжированный статистический ряд 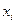
| |||||||||||||
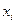
| 0.88 | 0.89 | 0.89 | 0.96 | 0.97 | 0.97 | 0.99 | 1.03 | 1.03 | 1.04 | 1.04 | 1.05 | 1.07 |
| 16 | ||||||
| 1.07 | 1.08 | 1.09 | 1.13 | 1.15 | 1.25 | 1.45 |
2. Выполняем точечную статистическую оценку выборки с использованием свойств математического ожидания и дисперсии
а) находим среднее выборки
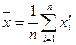
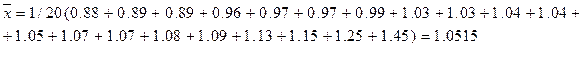
б) выборочная дисперсия
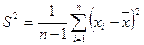

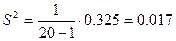
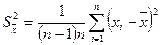
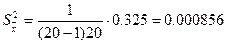
в) генеральная дисперсия
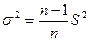
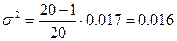
3. Проверка однородности наблюдений ( 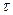 –критерий)
–критерий)
На наличие грубых погрешностей в результатах проверяются крайние элементы выборки 0.88 и 1.45.
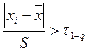 ,
,
где 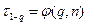
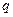 –принятый уровень значимости (
–принятый уровень значимости ( 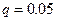 );
);
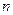 –объем выборки (20).
–объем выборки (20).
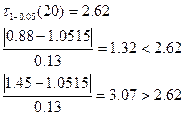
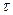 –критерий выполняется во втором случае, следовательно, из данной выборки исключаем крайний правый член – 1.45.
–критерий выполняется во втором случае, следовательно, из данной выборки исключаем крайний правый член – 1.45.
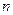
| |||||||||||||
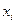
| 0.88 | 0.89 | 0.89 | 0.96 | 0.97 | 0.97 | 0.99 | 1.03 | 1.03 | 1.04 | 1.04 | 1.05 | 1.07 |
| 16 | |||||
| 1.07 | 1.08 | 1.09 | 1.13 | 1.15 | 1.25 |
а) находим среднее выборки
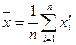
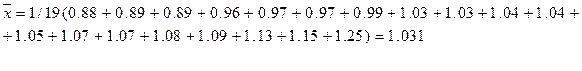
б) выборочная дисперсия
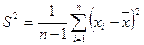

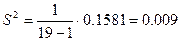
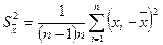
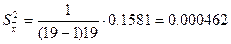
в) генеральная дисперсия
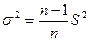
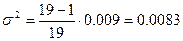
Заново проверяем на наличие грубых ошибок крайние элементы выборки 0.88 и 1.25:
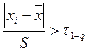 ,
,
где 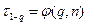
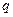 –принятый уровень значимости (
–принятый уровень значимости ( 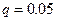 );
);
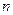 –объем выборки (19).
–объем выборки (19).
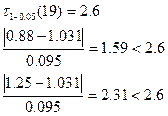
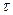 –критерий не выполняется в обоих случаях, следовательно, выборка не имеет грубых погрешностей.
–критерий не выполняется в обоих случаях, следовательно, выборка не имеет грубых погрешностей.
4. Построение вариационных рядов.
а) в виде таблицы
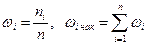
б) в виде графиков
1) кумулятивная кривая 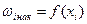 ;
;
2) полигон 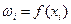 .
.
Т.к. вариационный ряд дискретный то гистограмму не строим.
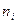 – частота интервала;
– частота интервала;
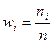 - частость интервала;
- частость интервала;
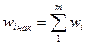 - накопленная частость интервала.
- накопленная частость интервала.
Таблица 3
Дискретный вариационный ряд
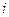
| 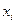
| 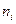
| 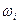
| 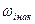
|
| 0,88 | 0.053 | 0.053 | ||
| 0,89 | 0.106 | 0.159 | ||
| 0,96 | 0.053 | 0.212 | ||
| 0,97 | 0.106 | 0.318 | ||
| 0,99 | 0.053 | 0,371 | ||
| 1,03 | 0,106 | 0.477 | ||
| 1,04 | 0.106 | 0.583 | ||
| 1,05 | 0.053 | 0.636 | ||
| 1,07 | 0.106 | 0.742 | ||
| 1,08 | 0.053 | 0.795 | ||
| 1,09 | 0.053 | 0.848 | ||
| 1,13 | 0.053 | 0.901 | ||
| 1,15 | 0.053 | 0.954 | ||
| 1,25 | 0.053 |
Кумулятивная кривая 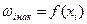 и полигон
и полигон 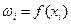 показаны в приложении на рисунках 1 и 2 соответственно.
показаны в приложении на рисунках 1 и 2 соответственно.
На основании полученных кривых выносим основную гипотезу о нормальном законе распределения выборки.
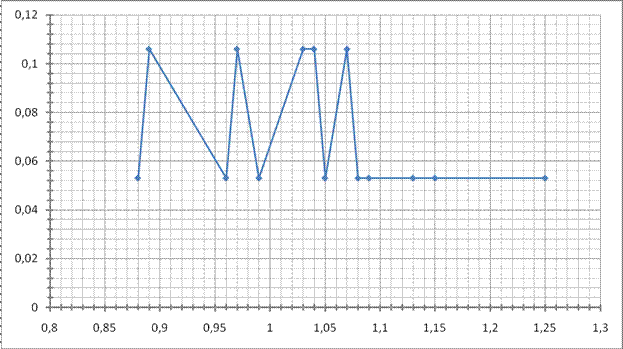
Рисунок 1. Полигон 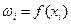
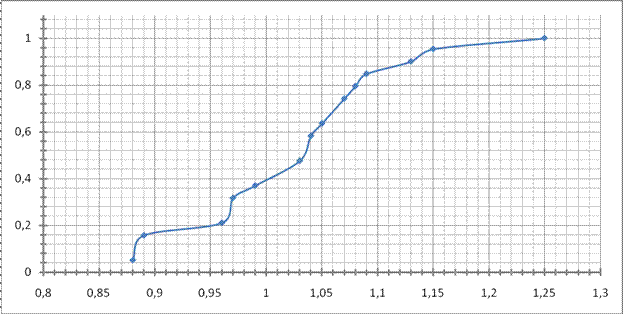
Рисунок 2. Кумулятивная кривая 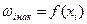
5. Проверка основной гипотезы о нормальности распределения.
5.1 Алгебраические критерии согласия:
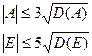
где 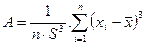 – асимметрия,
– асимметрия,
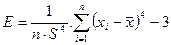 – эксцесс,
– эксцесс,
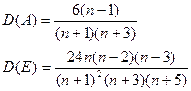
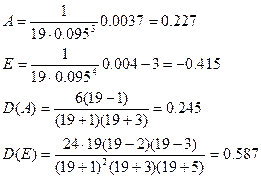

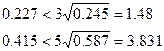
Т.к. оба критерия выполняются, то закон распределения выборки принимается нормальным.
5.2. Графический критерий согласия:
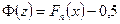
где 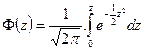 – интеграл Лапласа
– интеграл Лапласа
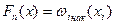
а) Строится таблица
Таблица 4
Значения аргумента 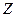 для
для 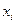
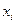
| 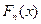
| 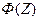
| 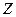
|
| 0,88 | 0.053 | -0.447 | -1,62 |
| 0,89 | 0.159 | -0.341 | -1 |
| 0,96 | 0.212 | -0.288 | -0,8 |
| 0,97 | 0.318 | -0.182 | -0,47 |
| 0,99 | 0.371 | -0.129 | -0,33 |
| 1,03 | 0.477 | -0.023 | -0,06 |
| 1,04 | 0.583 | 0.083 | 0,21 |
| 1,05 | 0.636 | 0.136 | 0,35 |
| 1,07 | 0.742 | 0.242 | 0,65 |
| 1,08 | 0.795 | 0.295 | 0,82 |
| 1,09 | 0.848 | 0.348 | 1,03 |
| 1,13 | 0.901 | 0.401 | 1,29 |
| 1,15 | 0.954 | 0.454 | 1,69 |
| 1,25 | 0.5 |
б) Строится график 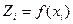 (Рисунок 3).
(Рисунок 3).
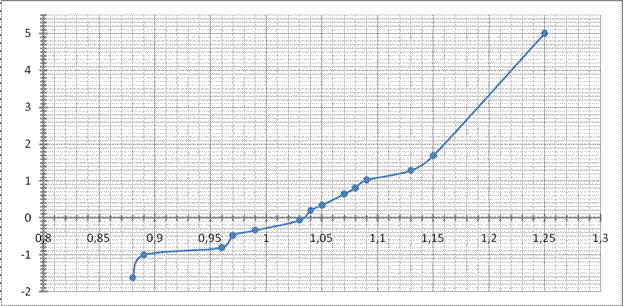
Рисунок 3. Z = f(x)
Т.к. точки 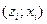 на графике располагаются вдоль одной прямой, то гипотеза о нормальном законе выборки принимается.
на графике располагаются вдоль одной прямой, то гипотеза о нормальном законе выборки принимается.
5.3. Графический критерий согласия на основе эмпирического распределения:
На графике статистической функции распределения эмпирической функции 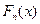 (кумулятивных кривых) строится график функции нормального распределения (теоретическая функция) (Рисунок 4).
(кумулятивных кривых) строится график функции нормального распределения (теоретическая функция) (Рисунок 4).
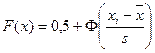 ,
,
где 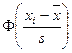 – функция Лапласа.
– функция Лапласа.
Таблица 5
Расчетные данные для 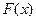
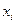
| 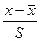 
| 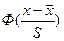
| 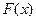
|
| 0,88 | -1.59 | -0.4441 | 0,0559 |
| 0,89 | -1.48 | -0.4306 | 0,0694 |
| 0,96 | -0.75 | -0.2734 | 0,2266 |
| 0,97 | -0.64 | -0.2389 | 0,2611 |
| 0,99 | -0.43 | -0.1664 | 0,3336 |
| 1,03 | -0.01 | -0.004 | 0,496 |
| 1,04 | 0.09 | 0.0359 | 0,5359 |
| 1,05 | 0.20 | 0.0793 | 0,5793 |
| 1,07 | 0.41 | 0.1591 | 0,6591 |
| 1,08 | 0.52 | 0.1985 | 0,6985 |
| 1,09 | 0.62 | 0.2324 | 0,7324 |
| 1,13 | 1.04 | 0.3508 | 0,8508 |
| 1,15 | 1.25 | 0.3944 | 0,8944 |
| 1,25 | 2.31 | 0.4896 | 0,9896 |
Визуально определяя расхождение между эмпирической и теоретической функциями распределения делаем вывод, что оно невелико, следовательно, принимаем гипотезу о нормальном законе распределения.
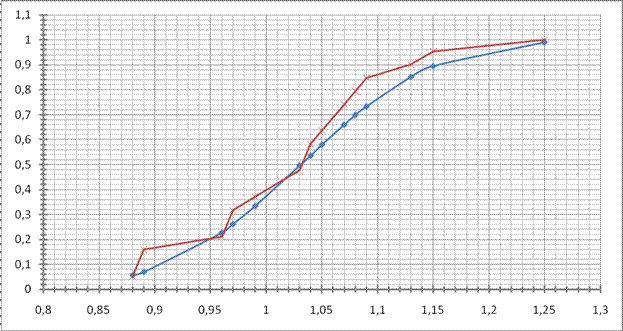
Рисунок 4. Кумулятивные кривые – эмпирическая функция распределения и теоретическая функция распределения (промаркированы крестиками – Fn(x), ромбиками - F(x))
5.4. Критерий согласия Колмогорова.
Используется для надежной количественной оценки основной гипотезы:
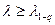
где 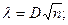
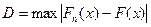
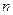 – объем выборки,
– объем выборки,
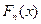 – статистическая функция распределения,
– статистическая функция распределения,
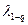 – квантиль Колмогорова (
– квантиль Колмогорова ( 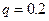 ).
).
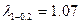
Таблица 6
Расчетные данные для 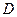
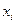
| 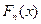
| 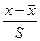 
| 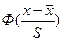
| 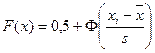
| 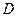
|
| 0.88 | 0.053 | -1.59 | -0.4441 | 0.0559 | 0.0029 |
| 0.89 | 0.159 | -1.48 | -0.4306 | 0.0694 | 0.0896 |
| 0.96 | 0.212 | -0.75 | -0.2734 | 0.2266 | 0.0146 |
| 0.97 | 0.318 | -0.64 | -0.2389 | 0.2611 | 0.0569 |
| 0.99 | 0.371 | -0.43 | -0.1664 | 0.3336 | 0.0374 |
| 1.03 | 0.477 | -0.01 | -0.004 | 0.496 | 0.019 |
| 1.04 | 0.583 | 0.09 | 0.0359 | 0.5359 | 0.0471 |
| 1.05 | 0.636 | 0.20 | 0.0793 | 0.5793 | 0.0567 |
| 1.07 | 0.742 | 0.41 | 0.1591 | 0.6591 | 0.0829 |
| 1.08 | 0.795 | 0.52 | 0.1985 | 0.6985 | 0.0965 |
| 1.09 | 0.848 | 0.62 | 0.2324 | 0.7324 | 0.1156 |
| 1.13 | 0.901 | 1.04 | 0.3508 | 0.8508 | 0.0502 |
| 1.15 | 0.954 | 1.25 | 0.3944 | 0.8944 | 0.0596 |
| 1.25 | 2.31 | 0.4896 | 0.9896 | 0.0104 |
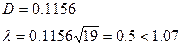
Критерий Колмогорова не выполняется, значит, основная гипотеза принимается, закон распределения нормальный.
6. Интервальная (квантильная) оценка выборки.
а) генерального среднего “a”:
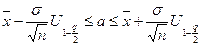 ,
,
где 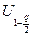 – квантиль стандартного нормального распределения (
– квантиль стандартного нормального распределения ( 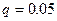 ).
).
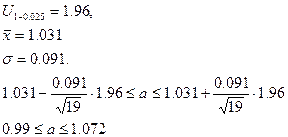
б) Генеральной дисперсии “σ”:
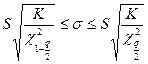 ,
,
где 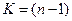 – число степеней свободы выборки;
– число степеней свободы выборки;
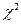 – квантили Пирсона (
– квантили Пирсона ( 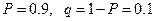 ).
).
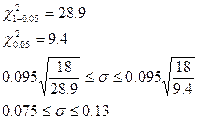
7. Окончательные результаты.
Выборка распределена по нормальному закону.
Точечная оценка выборки:
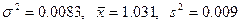
Интервальные оценки выборки:
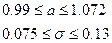
При Рд = 0.9
Вывод: использовав ряд критериев, мы убедились, что высказанная ранее гипотеза о нормальном распределении данной выборки является верной.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|