- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКАЯ РАБОТА. ОБУЧАЮЩАЯ ТАБЛИЦА
ПРАКТИЧЕСКАЯ РАБОТА
«Применение интеграла для вычисления площадей и объемов»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Применение определенного интеграла для вычисления площадей и объемов».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблицы первообразных некоторых функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
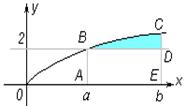
а) Какую фигуру называют криволинейной трапецией? Приведите примеры криволинейных трапеций.
б) Запишите формулу для вычисления площади криволинейной трапеции.
в) Покажите на рисунках и запишите интегральные формулы, с помощью которых можно вычислить площади фигур, не являющихся криволинейными трапециями.
г) Запишите и с помощью иллюстрации прокомментируйте интегральную формулу для вычисления объемов тел.
2. С помощью обучающей таблицы повторить план вычисления площади криволинейной трапеции и изучить образцы решенных задач.
3. Выполнить задания для самоконтроля (в таблице).
4. Изучить условие заданий для практической работы.
5. Оформить отчет о работе.
ОБУЧАЮЩАЯ ТАБЛИЦА
Определение. Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке 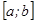 знака функции
знака функции 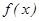 , прямыми
, прямыми 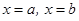 и отрезком
и отрезком 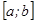 . Площадь S криволинейной трапеции находится по формуле
. Площадь S криволинейной трапеции находится по формуле
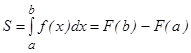 . (*)
. (*)
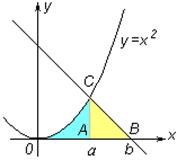
Задание. Вычислите площадь фигуры, ограниченной линиями:
а) 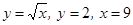 ; б)
; б) 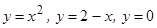 .
.
| № | План вычисления площади | Применение | плана | ||||
| шага | криволинейной трапеции | а) 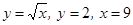
| б) 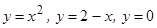
| ||||
| Строим заданные линии и штриховкой отмечаем фигуру, площадь которой надо найти. Установим, является ли эта фигура криволинейной трапецией | ||||||
| Записываем формулу для вычисления площади искомой фигуры | 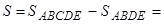
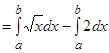
| 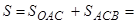
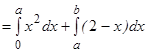
| |||||
| Находим пределы интегрирования | 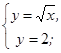 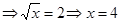 , ,
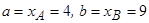
| 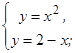 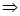 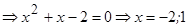
| |||||
| Вычисляем искомую площадь по формуле (*) | 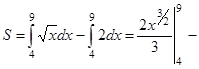
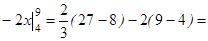 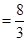 , ,
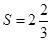 (кв.ед.) (кв.ед.)
| 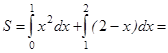
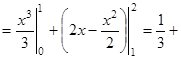
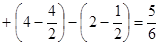 , ,
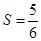 (кв.ед.) (кв.ед.)
|
Примеры. Вычислите площадь фигуры, ограниченной линиями:
1) 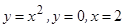 ; 2)
; 2) 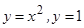 ; 3)
; 3) 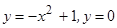 ; 4)
; 4) 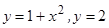 ;
;
5) 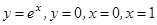 ; 6)
; 6) 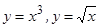 ; 7)
; 7) 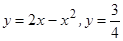 ; 8)
; 8) 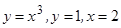 ;
;
9) 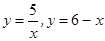 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|