
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ижевский ТЕХНИКУМ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА УДМУРТПОТРЕБСОЮЗА»
«Ижевский ТЕХНИКУМ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА УДМУРТПОТРЕБСОЮЗА»
| СОГЛАСОВАНО: Цикловая комиссия общеобразовательных дисциплин Протокол № __ от «__» ______ 20__ г. Председатель __________ А.П. Разина | Экзаменационный билет Вариант № 2 МАТЕМАТИКА | УТВЕРЖДАЮ: Заместитель директора по учебно-методической работе __________ Т.П. Зуева «__» _________ 20__ г. |
Инструкция:
Внимательно прочитайте задания.
Выполните задание в соответствии с заданными условиями.
Ознакомьтесь с критериями оценки
Рационально распределите время на выполнение заданий.
Вы можете воспользоваться таблицами производных и интегралов основных элементарных функций, формулами тригонометрии.
Время выполнения задания – 180 минут.
Задание:
1. Упростите выражение: 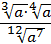 .
.
2. Решите уравнение: 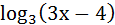 = 2.
= 2.
3. Решите неравенство: 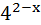
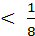 .
.
4. Найдите значение выражения: 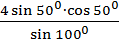 .
.
5. Найти наименьшее значение функции: y = 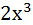 - 3x2 – 12x+ 1 на отрезке
- 3x2 – 12x+ 1 на отрезке 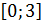 .
.
6. Найдите первообразную функции f(x) = x2 +4x график которой проходит через точку А(3;2).
7. В мешке содержится жетоны с номером от 1 до 50 включительно. Какова вероятность того, что извлеченный наугад из мешка жетон содержит только одну цифру 3? Результат округлить до десятых.
8. В прямоугольном параллелепипеде АВСДА1В1С1Д1 известно, что ВД=5см, АД=3см, АА1=6см. Найдите площадь боковой поверхности.
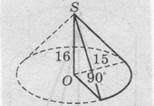
9. Найдите объем V части конуса, изображенного на рисунке. В ответе укажите 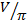 .
.
10. Решите уравнение: 2sin2x – 3sinx +1 = 0. Найдите все корни уравнения, принадлежащие отрезку 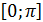 .
.
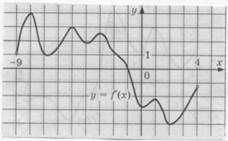
11. На рисунке изображен график производной функции f(х), определенной на интервале (-9;4). Найдите точку экстремума функции f(х) на отрезке [-2;3].
КРИТЕРИИ ОЦЕНКИ
Каждое задание оценивается определенным количеством баллов, указанных в таблице:
| № задания | Максимальное количество баллов | Критерии |
| 10 баллов присваивается, если правильно найдено решение. 8 баллов присваивается, если правильно применены свойства корня и степени но допущена ошибка в вычислениях. 4 баллов присваивается, если допущена ошибка в свойствах корня. 2 балла присваивается, если допущена ошибка в свойствах степени, но правильно применены свойства корня. | ||
| 8 баллов присваивается, если правильно найдено решение. 4 балла присваивается, если правильно применены свойства логарифмов, но допущена вычислительная ошибка. 2 балла присваивается, если допущена ошибка в свойствах логарифмов. | ||
| 10 баллов присваивается, если верно найдено решение. 6 баллов присваивается, если верно применены свойства показательной функции, но допущена ошибка в вычислениях или записи ответа. 4 балла присваивается, если допущена ошибка в свойствах показательной функции. 2 баллов присваивается, если общая идея, способ решения верны, но не верно выполнен переход к одному основанию. | ||
| 8 баллов присваивается, если верно найдено решение. 4 балла присваивается, если верно применена формула синуса двойного угла, но допущена ошибка в вычислениях. 2 балла присваивается, если при применении формулы синуса двойного угла допущена ошибка. | ||
| 10 баллов присваивается, если верно и полностью найдено решение. 8 баллов присваивается, если верно применены формулы и правила дифференцирования; верно найдены корни квадратного уравнения, но допущена ошибка в вычислениях. 5 баллов присваивается, если верно применены формулы дифференцирования, но допущена ошибка при решении квадратного уровня. 2 балла присваивается, если общая идея способ решения, но не выполнены некоторые промежуточные этапы решения | ||
| 10 баллов присваивается, если верно найдено решение. 8 баллов присваивается, если верно применены формулы первообразных и найдены найден общий вид первообразных, но допущена ошибка в вычислениях. 5 баллов присваивается, если при нахождении первообразной допущена 1 ошибка. 2 балла присваивается, если приведена неполная последовательность шагов решения. | ||
| 8 баллов присваивается, если верно найдено решение. 6 баллов присваивается, если верно приведены все этапы решения, но не верно применено правило округления чисел. 4 балла присваивается, если допущена ошибка в вычисления при правильном ходе решения задачи. 2 балла присваивается, если допущена ошибка при нахождении числа благоприятных исходов. | ||
| 10 баллов присваивается, если верно выполнен рисунок и найдено верное решение. 8 баллов присваивается, если верно применены формулы площадей поверхностей многогранников, но допущена вычислительная ошибка. 5 баллов присваивается, если верно приведены все шаги решения, но не верно выполнен рисунок. 2 балла присваивается, если решение не завершено или допущены ошибки в формулах. | ||
| 8 баллов присваивается, если верно найдено решение. 6 баллов присваивается, если верно применены формулы объема тел вращения и его частей, но допущена ошибка в вычислениях. 4 балла присваивается, если верно найден объём всего тела вращения, но допущена ошибка при нахождении объёма части тела вращения. 2 балла присваивается, если ход решения задачи верный, но задача не завершена. | ||
| 10 баллов присваивается, если верно найдено решение. 8 баллов присваивается, если верно приведено решение тригонометрического уравнения, но допущена ошибка при нахождении корней из отрезка. 5 баллов присваивается, если верно решено уравнение, но не найдены корни из отрезка. 2 балла присваивается, если допущена ошибка при решении уравнения. | ||
| 8 баллов присваивается, если верно найдено решение с полным обоснованием. 4 балла присваивается, если при верном обосновании не верно назван ответ. 2 балла присваивается, если верно назван ответ, но нет обоснования |
Баллы суммируются и переводятся в оценку по пятибалльной шкале:
| Процент результативности (правильных ответов) | Качественная оценка индивидуальных образовательных достижений | |
| балл (отметка) | вербальный аналог | |
| 90 ÷ 100 | отлично | |
| 80 ÷ 89 | хорошо | |
| 70 ÷ 79 | удовлетворительно | |
| менее 70 | не удовлетворительно | |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|