
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«ЛУГАНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ИМЕНИ ВЛАДИМИРА ДАЛЯ»
Кафедра прикладной математики
Математическое моделирование
О Т Ч Ё Т
о выполнении практической работы № 7-8
ВЕРОЯТНОСТНОЕ МОДЕЛИРОВАНИЕ
Вариант № 0
Выполнил: студент группы
ФИО________________________
Дата сдачи____________________
Оценка______________________________
Проверил___________________________
Луганск, 2020
Выполнение работы
Задание 1. Смоделировать 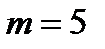 экспериментов по схеме Бернулли: эксперимент состоит из
экспериментов по схеме Бернулли: эксперимент состоит из 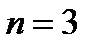 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 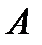 равна
равна 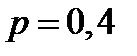 .
.
Решение.1) Пусть дискретная случайная величина 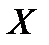 – число появлений события
– число появлений события 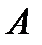 в трёх независимых испытаниях схемы Бернулли, в каждом из которых вероятность появления события
в трёх независимых испытаниях схемы Бернулли, в каждом из которых вероятность появления события 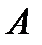 равна
равна 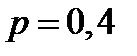 . Возможные значения случайной величины
. Возможные значения случайной величины 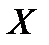 : 0,1,2,3. Соответствующие вероятности находятся по формуле Бернулли:
: 0,1,2,3. Соответствующие вероятности находятся по формуле Бернулли:
, , , .
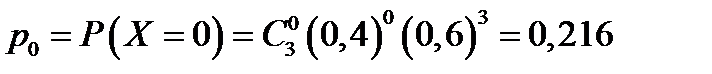 ,
,
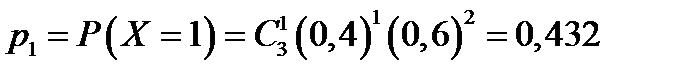 ,
,
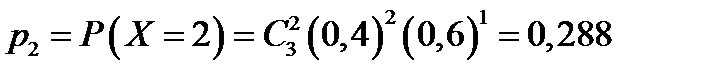 ,
,
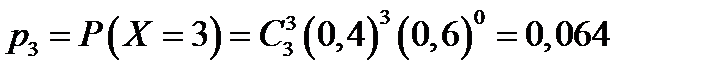 ,
,
Построим закон распределения случайной величины 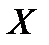 :
:
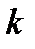
| 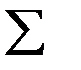
| ||||
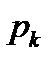
| 0,216 | 0,432 | 0,288 | 0,064 |
2) Смоделируем 5 возможных значений случайной величины 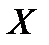 . Одно испытание – это выбор 5-и чисел из таблицы случайных чисел.
. Одно испытание – это выбор 5-и чисел из таблицы случайных чисел.
Разобьём интервал 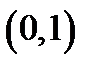 точками с координатами 0,216; 0,216+0,432=0,648, 0,216+0,432+0,288=0,936, на 4 частичных интервалов:
точками с координатами 0,216; 0,216+0,432=0,648, 0,216+0,432+0,288=0,936, на 4 частичных интервалов: 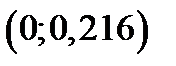 ,
, 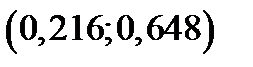 ,
, 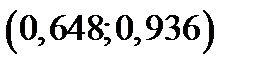 ,
, 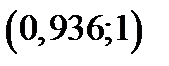 .
.
Выберем из таблицы равномерно распределенных случайных чисел любое число, например, 0,34. Случайное число 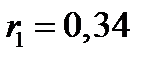 принадлежит частичному интервалу
принадлежит частичному интервалу 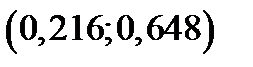 , поэтому дискретная случайная величина
, поэтому дискретная случайная величина 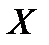 , которая моделируется, приняла возможное значение
, которая моделируется, приняла возможное значение 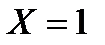 .
.
Аналогично выберем
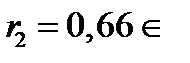
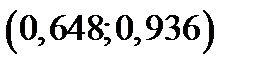 , поэтому
, поэтому 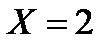 ;
;
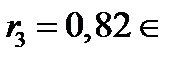
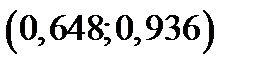 , поэтому
, поэтому 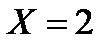 ;
;
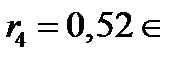
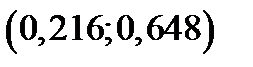 , поэтому
, поэтому 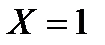 ;
;
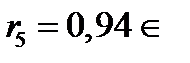
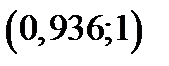 , поэтому
, поэтому 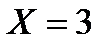 .
.
Таким образом, смоделированные возможные значения случайной величины 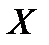 :1, 2, 2, 1, 3.
:1, 2, 2, 1, 3.
Задание 2.Смоделировать 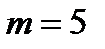 экспериментов, в каждом из которых происходит одно из событий
экспериментов, в каждом из которых происходит одно из событий 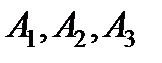 , которые образуют полную группу:
, которые образуют полную группу: 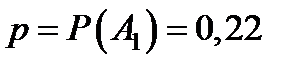 ,
, 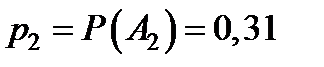 ,
, 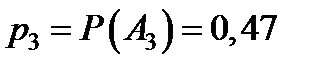 .
.
Решение.Рассмотрим ДСВ 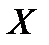 с законом распределения
с законом распределения
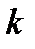
| 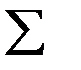
| |||
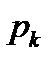
| 0,22 | 0,31 | 0,47 |
Смоделируем 5 возможных значений случайной величины 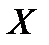 . Одно испытание – это выбор 5-и чисел из таблицы случайных чисел.
. Одно испытание – это выбор 5-и чисел из таблицы случайных чисел.
Разобьём интервал 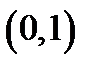 точками с координатами 0,22; 0,22+0,31=0,53, на 3 частичных интервалов:
точками с координатами 0,22; 0,22+0,31=0,53, на 3 частичных интервалов:  ,
, 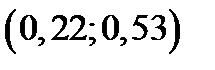 ,
, 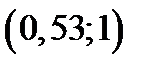 .
.
Выберем из таблицы случайных чисел любое число, например, 0,65. Случайное число 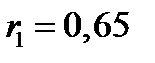 принадлежит частичному интервалу
принадлежит частичному интервалу 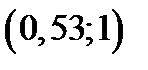 , поэтому дискретная случайная величина
, поэтому дискретная случайная величина 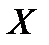 , которая моделируется, приняла возможное значение
, которая моделируется, приняла возможное значение 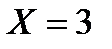 . Следовательно, произошло событие
. Следовательно, произошло событие 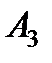 .
.
Аналогично
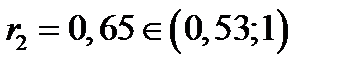 , поэтому
, поэтому 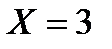 . Следовательно, произошло событие
. Следовательно, произошло событие 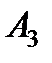 .
.
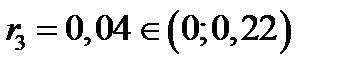 , поэтому
, поэтому 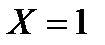 . Следовательно, произошло событие
. Следовательно, произошло событие 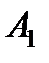 .
.
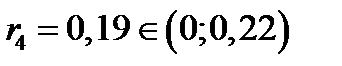 , поэтому
, поэтому 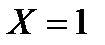 . Следовательно, произошло событие
. Следовательно, произошло событие 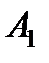 .
.
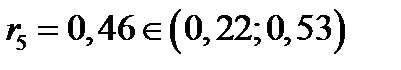 , поэтому
, поэтому 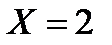 . Следовательно, произошло событие
. Следовательно, произошло событие 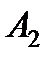 .
.
Таким образом, смоделирована следующая последовательность событий: 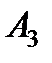 ,
, 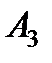 ,
, 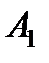 ,
, 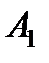 ,
, 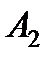 .
.
Задание 3. Смоделировать 4 возможных значений НСВ 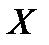 , распределенной равномерно на отрезке
, распределенной равномерно на отрезке 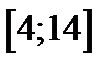 .
.
Решение.Воспользуемся методом обратной функции. Вычислим функцию распределения
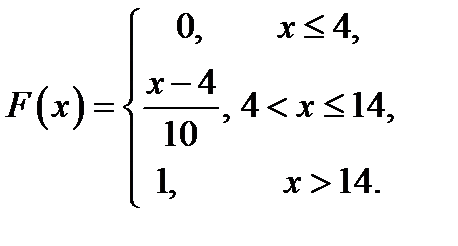
и приравняем её к значению 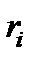 :
:

Откуда находим формулу для моделирования возможных значений НСВ 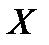 :
:
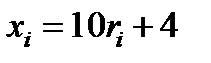 .
.
Выберем из таблицы случайных чисел любое число, например, 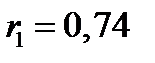 . Тогда
. Тогда
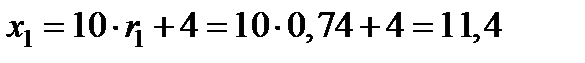
Аналогично,
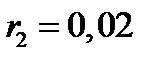 ,
, 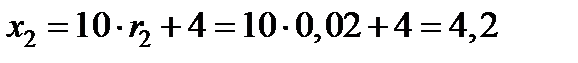 ;
;
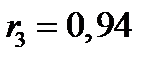 ,
, 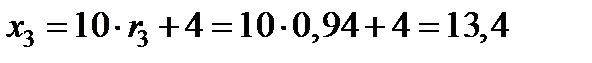 ;
;
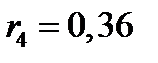 ,
, 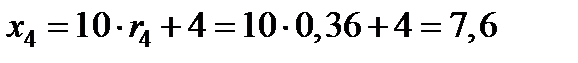 ;
;
Таким образом, смоделированы возможные значения случайной величины 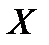 :
:
11,4; 4,2; 13,4; 7,6.
Задание 4. Смоделировать 5 возможных значений НСВ 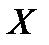 , распределенной экспоненциально с параметром
, распределенной экспоненциально с параметром 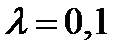 .
.
Решение.Воспользуемся методом обратной функции. Поскольку плотность имеет вид 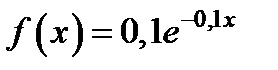 , то вычислим функцию распределения и приравняем её к значению
, то вычислим функцию распределения и приравняем её к значению 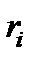 :
:
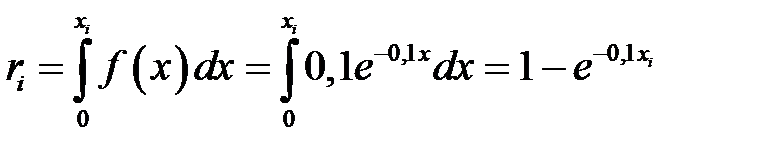 .
.
Откуда находим формулу для моделирования возможных значений НСВ 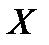 :
:
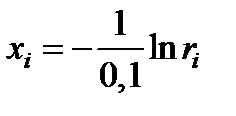 .
.
Выберем из таблицы случайных чисел любое число, например, 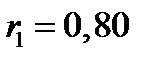 . Тогда
. Тогда
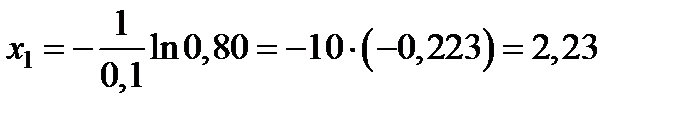
Аналогично,
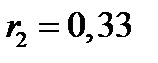 ,
, 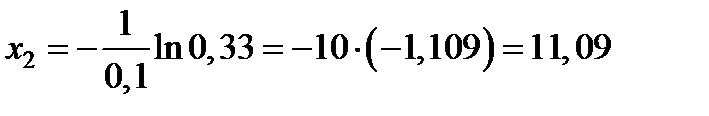 ;
;
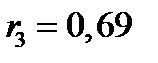 ,
, 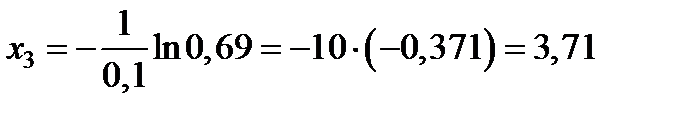 ;
;
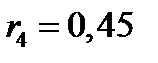 ,
, 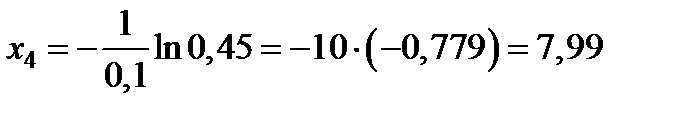 ;
;
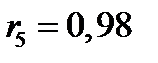 ,
, 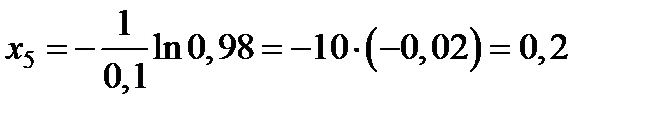 .
.
Таким образом, смоделированы возможные значения случайной величины 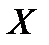 :
:
2,23; 11,09; 3,71; 7,99; 0,2.
Задание 5. Смоделировать 4 возможных значений НСВ 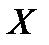 , распределенной нормально с параметрами
, распределенной нормально с параметрами 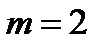 и
и 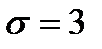 .
.
Решение.Сначала смоделируемвозможные значения НСВ 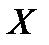 , распределенной нормально с параметрами
, распределенной нормально с параметрами 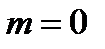 и
и 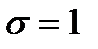 (стандартно). Для этого вычислим сумму
(стандартно). Для этого вычислим сумму
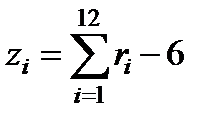
Выберем из таблицы случайных чисел 12 случайных чисел 0,37; 0,54; 0,20; 0,48; 0,05; 0,64; 0,89; 0,47; 0,42; 0,96; 0,24; 0,80 (первые 12 чисел из второй строки таблицы). Вычислим их сумму и получим:
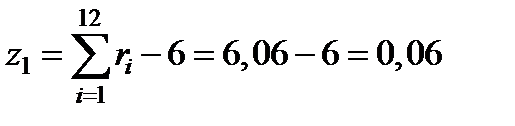 .
.
Аналогично, выбрав 12 случайных чисел из 3, 4 и 5 строки таблицы случайных чисел, получим:
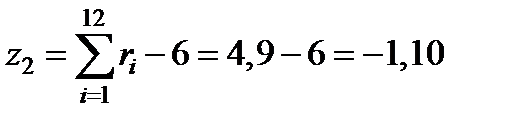 ,
,
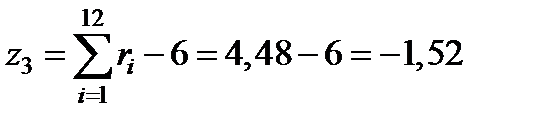 ,
,
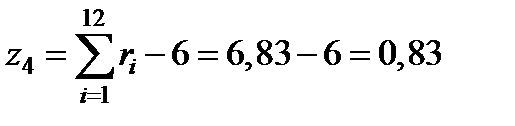 .
.
Найдем возможные значения НСВ 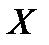 , распределенной нормально с параметрами
, распределенной нормально с параметрами 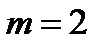 и
и 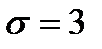 по формуле:
по формуле:
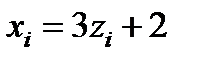 .
.
Получим:
 ,
,
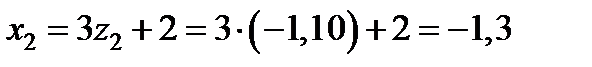 ,
,
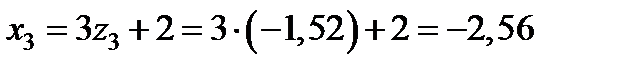 ,
,
 .
.
Таким образом, смоделированы возможные значения случайной величины 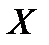 :
:
2,18; –1,3; –2,56; 4,49.
Задание 6. Используя результаты 100 имитационных прогонов для оценки времени (в мин.) пребывания посетителей в системе:
1) построить интервальный статистический ряд, разбив область реализаций на 8 одинаковых интервалов;
2) вычислить оценки для математического ожидания, дисперсии, среднего квадратического отклонения;
3) построить гистограмму частот.
Решение. 1) Построим интервальный статистический ряд, разбив область реализаций на 8 одинаковых интервалов. Вычислим длину частичного интервала:
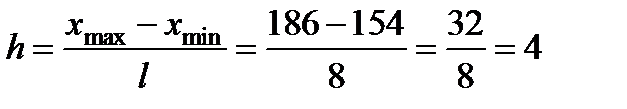 .
.
Тогда
| интервалы | [154-158) | [158-162) | [162-166) | [166-170) | [170-174) | [174-178) | [178-182) | [182-186) |
частоты 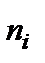
|
Замечание. Построить интервальный статистический ряд можно воспользовавшись встроенной функцией математического пакета Mathcad, которая позволяет отсортировать вектор выборочных данных V и имеет формат sort(V).
2) Вычислим оценки для выборочной средней, дисперсии, среднего квадратического отклонения. Для этого перейдем от интервального статистического ряда к дискретному, вариантами которого являются середины частичных интервалов.
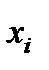
| ||||||||
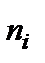
|
Оценка математического ожидания:
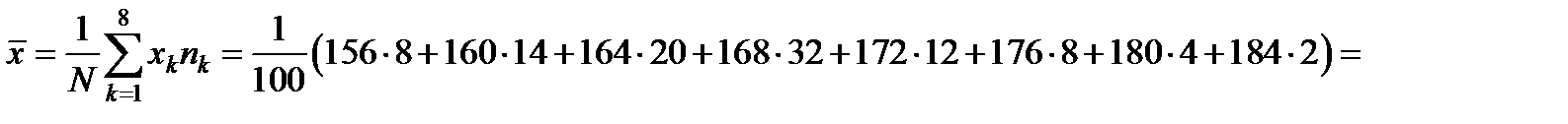
=167,04.
Оценка дисперсии:
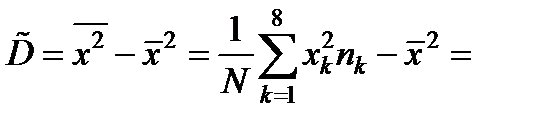

Оценка среднего квадратического отклонения:
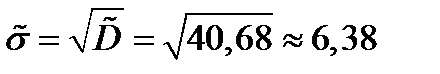 .
.
3) Построим гистограмму частот.
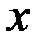
|
| 0,04 |
| 0,08 |
| 0,12 |
| 0,20 |
| 0,32 |
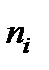
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|