Метод равномерного поиска

Метод равномерного поиска

Дана функция f(x)=5(x^2-x)sinx, а=0, в=3,2, малое положительное число=0,001. Затабулируем данную функцию и приведем ее к виду =5*(A1^2-A1)*SIN(A1).

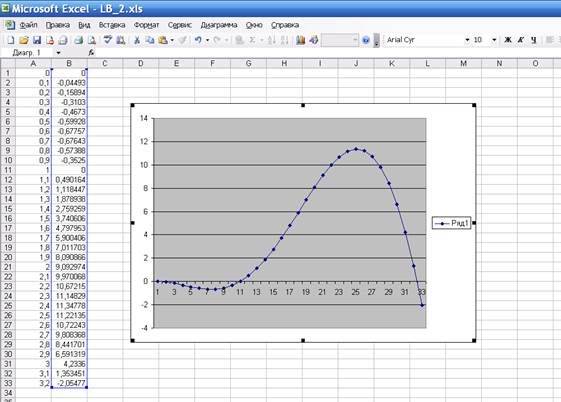
Покрою отрезок [a,b] сеткой равномерных узлов с точками 0; 0,1; 0,2; 0,3; 0,4;….;3,2.

Шаг 1:

1. x⁰=a=0, x^h=b=3,2, n=32,

h= 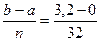=0,1

xⁱ=0+i*0,1

2. Вычисляем значения функции в каждой точке и находим среди них максимальную.

1) f(0,1)= -0,04493

2) f(0,2)= -0,15894

3) f(0,3)= -0,3103

4) f(0,4)= -0,4673

5) f(0,5)= -0,59928

6) f(0,6)= -0,67757

7) f(0,7)= -0,67643

8) f(0,8)= -0,57388

9) f(0,9)= -0,3525

10) f(1)=0

11) f(1,1)= 0,490164

12) f(1,2)= 1,118447

13) f(1,3)= 1,878938

14) f(1,4)=2,759259

15) f(1,5)= 3,740606

16) f(1,6)= 4,797953

17) f(1,7)= 5,900406

18) f(1,8)= 7,011703

19) f(1,9)= 8,090866

20) f(2)= 9,092974

21) f(2,1)= 9,970068

22) f(2,2)= 10,67215

23) f(2,3)= 11,14829

24) f(2,4)= 11,34778

25) f(2,5)= 11,22135

26) f(2,6)= 10,72243

27) f(2,7)= 9,808368

28) f(2,8)= 8,441701

29) f(2,9)= 6,591319

30) f(3)= 4,2336

31) f(3,1)= 1,353451

32) f(3,2)= -2,05477

f(x^k)=mах{0;………; -2,05477 )

Минимальная точка функции достигается при х= 3,2, т. е. f(2,4)= 11,34778

3. 2,4 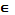[2,3; 2,5]

4. a=2,3; b=2,5

|2,5 – 2,3|<0,001,

0,2<0,001, неверное, следовательно, идём к пункту №1.

Шаг 2:

1. x⁰=a=2,3, x^h=b=2,5, n=10,

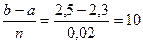
xⁱ=2,3+i*2,5

2. Вычисляем значения функции в каждой точке и находим среди них максимальную.

1) f(2,32)= 11,21193

2) f(2,34)= 11,26409

3) f(2,36)= 11,30438

4) f(2,38)= 11,33241

5) f(2,4)= 11,34778

6) f(2,42)= 11,35011

7) f(2,44)= 11,339

8) f(2,46)= 11,31409

9) f(2,48)= 11,275

10) f(2,5)= 11,22135

f (x^k)=max{11,21193;………; 11,22135)

Максимальная точка функции достигается при х= 2,42, т. е. f(2,42)= 11,35011

3. 2,42 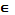[2,4; 2,44]

4. a=2,4; b=2,44

|2,44 – 2,4|<0,001,

0,04<0,001, неверное, следовательно идём к пункту №1.

Шаг 3:

1. x⁰=a=2,4, x^h=b=2,44, n=5,

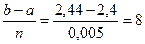
xⁱ=2,4+i*2,44

2. Вычисляем значения функции в каждой точке и находим среди них максимальную.

1) f(2,405)= 11,3496

2) f(2,41)= 11,3506

3) f(2,415)= 11,35077

4) f(2,42)= 11,35011

5) f(2,425)= 11,3486

6) f(2,43)= 11,34626

7) f(2,435)= 11,34306

8) f(2,44)= 11,339

f (x^k)=max{11,34778;………; 11,339)

Максимальная точка функции достигается при х=2,415, т. е. f(2,415)= 11,35077

3. 2,415 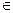[2,41; 2,42]

4. a=2,41; b=2,42

| 2,42 – 2,41 |<0,01,

0,01<0,001,неверное, следовательно, идём к пункту №1