Практическое занятие №12История и перспективы развития диагностического приборостроения

Практическое занятие №12"История и перспективы развития диагностического приборостроения"

Задача 1:
Амперметром класса точности 2.0 со шкалой (0…50) А измерены значения тока 0; 5; 10; 20; 25; 30; 40; 50 А. Рассчитать зависимости абсолютной, относительной и приведѐнной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

Для записи результатов формируем таблицу, в столбцы которой будем записывать измеренные значения I, абсолютные DI, относительные dI и приведенные gI погрешности.

В первый столбец записываем заданные в условии задачи измеренные значения тока: 0, 5, 10, 20, 25, 30, 40, 50 А.

Класс точности амперметра задан числом без кружка, следовательно, приведенная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |gI|£2%.

При решении задачи рассмотрим худший случай |gI|=2%, когда приведенная погрешность принимает максимальное по абсолютной величине значение, что соответствует gI=+2% и gI=-2%.

Рассчитаем значения абсолютной погрешности.

Из формулы 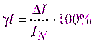выражаем абсолютную погрешность . За нормирующее значение I_N принимаем размах шкалы, т.к. шкала амперметра содержит нулевую отметку, т. е. I_N=|50 А – 0 А| = 50 А.

Абсолютная погрешность равна во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.

. При I=0 A получаем: . При I=5 A получаем: .

Значения относительной погрешности для остальных измеренных значений тока рассчитываются аналогично.

Учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной DI, относительной dI и приведенной gI погрешностей от результата измерений I .

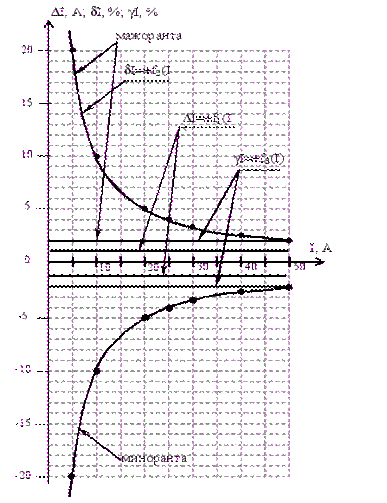
Графики зависимостей абсолютной, относительной и приведенной погрешностей от результата измерений для прибора с преобладающими аддитивными погрешностями

Задача 2:
Вольтметром класса точности 0,5 (значение класса точности указано в круге) со шкалой (0…100) В измерены значения напряжения 0; 10; 20; 40; 50; 60; 80; 100 В. Рассчитать зависимости абсолютной и относительной погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

Для записи результатов формируем таблицу в столбцы которой будем записывать измеренные значения V, абсолютные DV и относительные dV погрешности.

В первый столбец записываем заданные в условии задачи измеренные значения тока: 0, 10, 20, 40, 50, 60, 80, 100 (В).

Класс точности вольтметра задан числом в кружке, следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |dV|£0,5%.

При решении задачи рассмотрим худший случай, т.е. |dV|=0,5%, что соответствует значениям dV=+0,5% и dV=-0,5%

Примем во внимание опыт решения задачи 5.2., из которого видно, что результаты вычисления, выполненные для положительных и отрицательных значений погрешностей, численно совпадают друг с другом и отличаются только знаками "+" или "-". Поэтому дальнейшие вычисления будем производить только для положительных значений относительной погрешности dV=0,5%, но при этом будем помнить, что все значения второго и третьего столбцов таблицы 2.2. могут принимать и отрицательные значения.

З начение относительной погрешности dV=0,5% заносим в третий столбец таблицы.

Рассчитаем значения абсолютной погрешности.

Из формулы 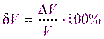выражаем абсолютную погрешность:

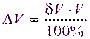При V=0 В получаем: .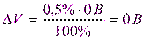

При V=10 В получаем:

Значения абсолютной погрешности для остальных измеренных значений напряжения рассчитываются аналогично.

Полученные таким образом значения абсолютной погрешности заносим во второй столбец.

По данным таблицы 2.2, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной DV и относительной dV погрешностей от результата измерений V (см. рис. 3).

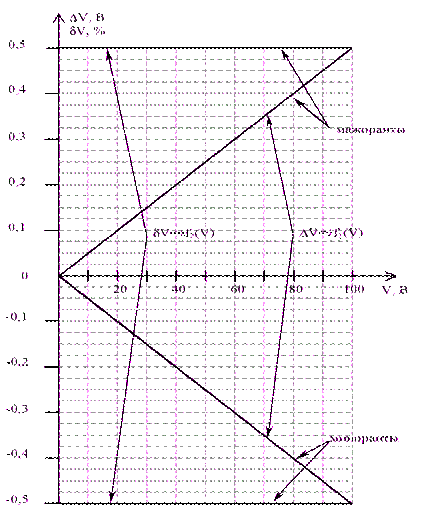
Графики зависимостей абсолютной и относительной погрешностей от результата измерений для прибора с преобладающими мультипликативными погрешностями

Задача 3:
Цифровым омметром класса точности 1.0/0.5 со шкалой (0...1000) Ом измерены значения сопротивления 0; 100; 200; 400; 500; 600; 800; 1000 Ом. Рассчитать зависимости абсолютной и относительной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

Для записи результатов формируем таблицу, в столбцы которой будем записывать измеренные значения R, абсолютные DR и относительные dR погрешности.

В первый столбец записываем заданные в условии задачи измеренные значения сопротивления: 0, 100, 200, 400, 500, 600, 800, 1000 (Ом).

К ласс точности вольтметра задан в виде двух чисел, разделенных косой чертой. Следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы должна удовлетворять следующему соотношению:

, %.

В данном случае, а=1,0; b=0,5; R_к=1000 Ом, причем параметры этой формулы а и b ответственны, соответственно, за мультипликативную и аддитивную составляющие суммарной погрешности.

Таким образом, получаем:

При решении задачи рассмотрим худший случай

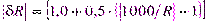что соответствует значениям .

Примем во внимание опыт решения задачи 5.2, из которого видно, что результаты вычисления, выполненные для положительных и отрицательных значений погрешностей, численно совпадают друг с другом и отличаются только знаками "+" или "-". поэтому дальнейшие вычисления будем производить только для положительных значений относительной погрешности 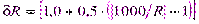, но при этом будем помнить, что все значения второго и третьего столбцов таблицы 2.3 могут принимать и отрицательные значения.

Рассчитаем значения относительной погрешности.

При R=0 Ом получаем: .

При R=100 Ом получаем: .

Значения относительной погрешности для остальных измеренных значений сопротивления рассчитываются аналогично.

Полученные значения относительной погрешности заносим в третий столбец таблицы 2.3.

Рассчитаем значения абсолютной погрешности.

Из формулы 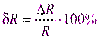выражаем абсолютную погрешность

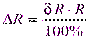. При R=0 Ом получаем: 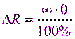– неопределенность.

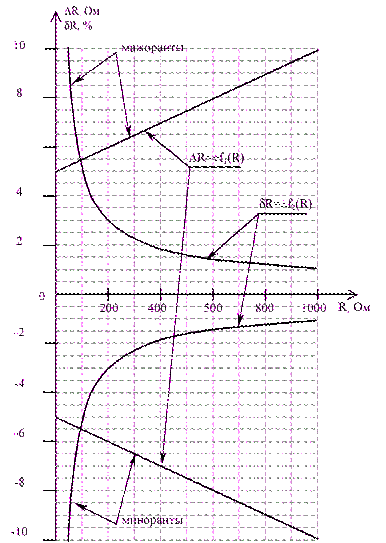
ВотГрафики зависимостей абсолютной и относительной погрешностей от результата измерений для прибора с соизмеримыми аддитивными и мультипликативными погрешностями

Искомое значение DR можно определить следующим образом. Так как класс точности прибора задан в виде двух чисел, то у данного прибора аддитивные и мультипликативные погрешности соизмеримы. При R=0 Ом мультипликативная составляющая погрешность равна нулю, значит, общая погрешность в этой точке обусловлена только аддитивной составляющей. Аддитивную составляющую представляет второе из чисел, задающих класс точности, т.е. в данном случае число b=0,5. Это означает, что аддитивная погрешность составляет 0,5% от верхнего предела измерений прибора, т.е. от R_к=1000 Ом.

Таким образом, при R=0 имеем .

При R=100 Ом получаем .

При R=200 Ом получаем .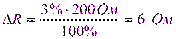

Значения абсолютной погрешности для остальных измеренных значений сопротивления рассчитываются аналогично. Полученные таким образом значения абсолютной погрешности заносим во второй столбец таблицы 2.3.

Контрольные вопросы:
1. Что называется классом точности средства измерений?

Класс точности средств измерений – обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность.

2. Какие существуют способы обозначения классов точности?

Обозначение классов точности вводится в зависимости от способов задания пределов допускаемых погрешностей. Возможны четыре варианта обозначения класса точности.

1) Если пределы допускаемой основной погрешности выражены в абсолютной форме, то класс точности средства измерения обозначают заглавными буквами латинского алфавита или римскими цифрами. Соответствие букв значению абсолютной погрешности раскрывается в технической документации на данное средство измерения. Обычно чем дальше буква от начала алфавита, тем больше значение допускаемой абсолютной.

2) Если пределы допускаемой основной погрешности выражены в приведенной форме , то класс точности средств измерений обозначается арабской цифрой, указывающей предел допускаемой погрешности. Например, класс точности прибора 1,5 означает, что g = ±1,5 %.

3) Если пределы допускаемой основной погрешности выражены в относительной форме, то класс точности средств измерений обозначается арабской цифрой в окружности, указывающей предел допускаемой погрешности. Например, класс точности прибора 0,5 означает, что d = ±0,5 %.

4) Если пределы допускаемой основной погрешности выражены в относительной форме, то класс точности средств измерений обозначается двумя цифрами, соответствующими значениям c и d.

3. Каким образом обозначается класс точности у средств измерений с преобладающей аддитивной составляющей погрешности?

Аддитивной называется погрешность абсолютное значение которой неизменно во всем диапазоне измеряемой величины.

Систематическая аддитивная погрешность смещает номинальную характеристику параллельно вверх или вниз на величину ±Dа.

Примером систематической аддитивной погрешности может служить погрешность от неточной установки прибора на нуль, от контактной э.д.с. в цепи постоянного тока. Аддитивную погрешность еще называют погрешностью нуля.

4. Каким образом обозначается класс точности у средств измерений с преобладающей мультипликативной составляющей погрешности?

Мультипликативнойназывают погрешность абсолютное значение которой изменяется пропорционально измеряемой величине.

При систематической мульти-пликативной погрешности реальная характеристика отклоняется от но-минальной вверх или вниз .

Примерами систематических мультипликативных погрешностей являются погрешности из-за изменения коэффициента деления делителя напряжения, из-за изменения жесткости пружины измерительного механизма и т.п. Мультипликативную погрешность еще называют погрешностью чувствительности.

5. Каким образом обозначается класс точности у средств измерений с соизмеримыми аддитивной и мультипликативной составляющими погрешности?

В средствах измерения аддитивные и мультипликативные погрешности, как правило, присутствуют одновременно. В этом случае результирующая погрешность определяется суммой аддитивной и мультипликативной погрешностей D = Dа+Dм= Dа+ dм × Х, где dм – относительная

мультипликативная погрешность. В зависимости от соотношений аддитивной (Dа) и мультипликативной (Dм) погрешностей классы точности средств измерений обозначаются по-разному. Можно выделить три характерных случая соотношения этих погрешностей 1) Dа = 0, Dм ¹ 0; 2) Dа ¹ 0, Dм = 0; 3) Dа @ Dм.

6. Каким образом обозначается класс точности у средств измерений с неравномерной шкалой?

Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например.

7. Что называется мажорантами и минорантами?

Мажоранта и миноранта это две функции, значения первой из которых не меньше, а второй не больше соответствующих значений данной функции (при всех рассматриваемых значениях независимой переменной).