ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ. При решении первой задачи применяется принцип ГЕОМЕТРИЧЕСКИХ МЕСТ ТОЧЕК на плоскости. СОПРЯЖЕНИЕ СТОРОН УГЛА ДУГОЙ ЗАДАННОГО РАДИУСА R. СОПРЯЖЕНИЕ ДУГИ ОКРУЖНОСТИ С ПРЯМОЙ ЛИНИЕЙ ДУГОЙ ЗАДАННОГО РАДИУСА r. Внешнее сопряжение дву

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

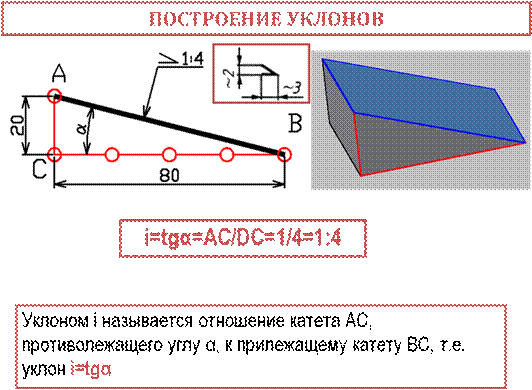
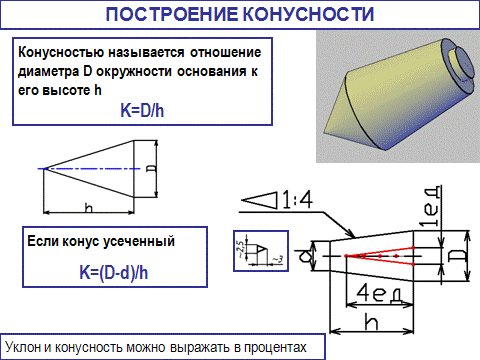
СОПРЯЖЕНИЕ –плавный переход одной линии в другую. Общая для этих линий точка называется

точкой сопряжения

При построении сопряжений решаются две основные задачи:

1 – определение центра сопрягающей дуги – Ц

2 – нахождение точек сопряжения – С1 и С2

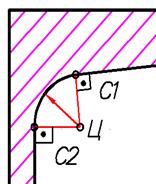
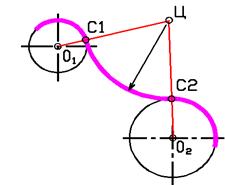Условия сопряжений линий:

1 – радиус дуги сопряжения, проведенный в точку касания прямой к окружности, перпендикулярен к прямой

2 - при касании дуг их центры и точка сопряжения лежат на одной прямой линии

При решении первой задачи применяется принцип ГЕОМЕТРИЧЕСКИХ МЕСТ ТОЧЕК на плоскости

ГМТ, равноудаленных от заданной прямой прямая параллельная заданной

ГМТ, равноудаленных от заданной окружности концентрическая окружность

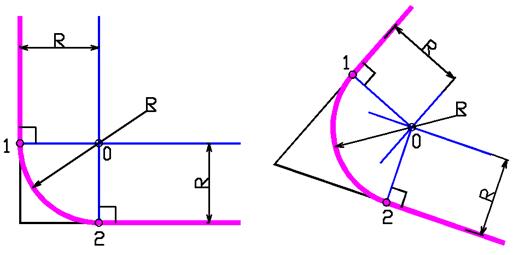
СОПРЯЖЕНИЕ СТОРОН УГЛА ДУГОЙ ЗАДАННОГО РАДИУСА R

Элементы сопряжения: R – радиус сопряжения ; 0 – центр сопряжения; 1,2 – точки сопряжения

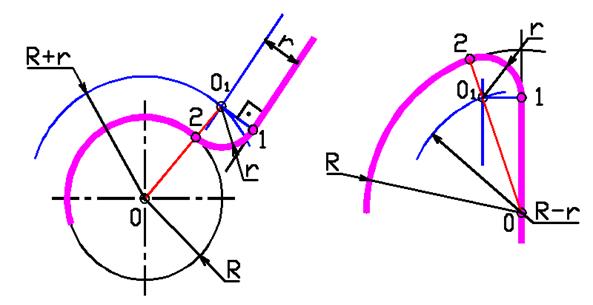
СОПРЯЖЕНИЕ ДУГИ ОКРУЖНОСТИ С ПРЯМОЙ ЛИНИЕЙ ДУГОЙ ЗАДАННОГО РАДИУСА r

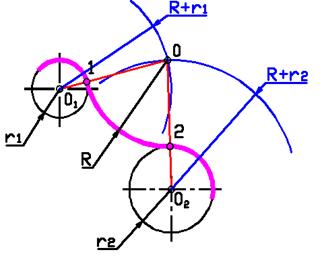
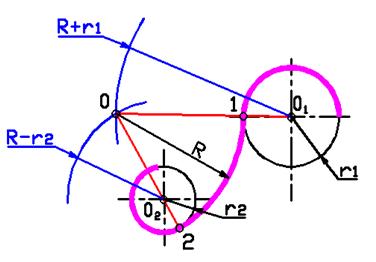
Внешнее сопряжение двух дуг дугой заданного радиуса R

При внешнем сопряжении центры 0₁ и 0₂ лежат вне сопрягающей дуги R

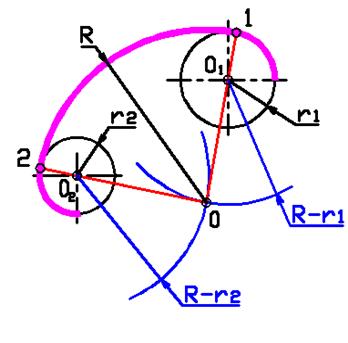
Внутреннее сопряжение двух дуг дугой заданного радиуса R

При внутреннем сопряжении центры 0₁ и 0₂ лежат внутри сопрягающей дуги R