
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Планування експерименту в задачах перевірки гіпотез
Критерії значимості

|
| Критерії значимості – це критерії, за допомогою яких перевіряються гіпотези про абсолютні значення параметрів чи про співвідношення між ними для генеральних сукупностей з відомої (з точністю до параметрів) функцією розподілу імовірностей. За допомогою різних критеріїв значимості можна: а) з'ясувати, чи не суперечать результати спостережень припущенню про те, що деякі з параметрів генеральної сукупності рівні цілком визначеним числам; б) якщо маються дві чи більша кількості вибірки, установити, чи існують об'єктивні підстави вважати, що вони є представниками однієї і тієї ж генеральної сукупності, чи ж експериментальні дані говорять про наявність невипадкових розходжень між вибірками, які свідчать про те, що вони витягнуті з різних генеральних сукупностей. |
| Розглянемо критерії значимості і довірчі інтервали. Якщо для теоретичного параметра генеральної сукупності Θ побудовано довірчий інтервал з рівнем значимості q, то цей інтервал можна застосувати для перевірки гіпотези щодо параметра Θ, якщо характер альтернативної гіпотези такий, що повинен бути використаний двосторонній критерій. Якщо гіпотетичне значення Θ0 попадає всередину довірчого інтервалу, нульова гіпотеза приймається з рівнем значимості q; якщо ж Θ0 лежить поза довірчим інтервалом, нульова гіпотеза відкидається. |
 Приклад 3.9. Нехай у прикладі 2.11 потрібно додатково перевірити гіпотези: Н0: m = 10 і Н1: m ≠ 10.
Так як гіпотетичне значення попадає всередину 95%-ного довірчого інтервалу, нульова гіпотеза повинна бути прийнята з рівнем значимості 0,05. Якби перевірялися гіпотези m = 0 і Н1: m ≠ 10, то Н0 варто було б відкинути, оскільки значення, що перевіряється, знаходиться поза довірчим інтервалом.
Приклад 3.9. Нехай у прикладі 2.11 потрібно додатково перевірити гіпотези: Н0: m = 10 і Н1: m ≠ 10.
Так як гіпотетичне значення попадає всередину 95%-ного довірчого інтервалу, нульова гіпотеза повинна бути прийнята з рівнем значимості 0,05. Якби перевірялися гіпотези m = 0 і Н1: m ≠ 10, то Н0 варто було б відкинути, оскільки значення, що перевіряється, знаходиться поза довірчим інтервалом.
|
Планування експерименту в задачах перевірки гіпотез

Рішення в даному випадку зводиться до визначення необхідного обсягу вибірки, який можна однозначно визначити, якщо зазначені:
1) припустимі значення імовірностей помилок першого і другого родів q і β;
2) відхилення d досліджуваного параметра Θ від гіпотетичного значення Θ0: d = Θ - Θ0, що бажано знайти в результаті перевірки.
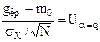 (3.1)
(3.1)
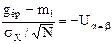 (3.2)
(3.2)
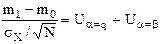 (3.3)
(3.3)
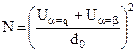 , (3.4)
де d0 — величина розбіжності між m1 і m0, яку треба знайти, у відносному масштабі:
, (3.4)
де d0 — величина розбіжності між m1 і m0, яку треба знайти, у відносному масштабі:
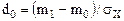 (3.5)
(3.5)
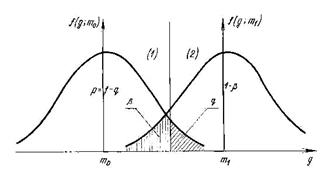 |
Рисунок 3.6 - До визначення розміру вибірки.
Природньо, що одержуване значення N повинно бути округлене до найближчого більшого цілого числа.
Формула (3.4) справедлива і для випадку, коли m1<m0 (№ 2 по табл. 3.2). Якщо використовується двосторонній критерій (№ 1 по табл. 3.2), то всі міркування лише не набагато складніші вищенаведених.
Приклад 3.10. Досліджується міцність металу на розрив. Визначити необхідне число дослідів для виявлення зростання міцності, рівного половині середньоквадратичного відхилення.
Оскільки які-небудь додаткові вимоги відсутні, задамося q = β = 0,05. За умовою d0 = 0,5. За допомогою таблиць нормального розподілу знаходимо 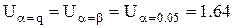 . Тоді N = 43, отже, для рішення поставленої задачі необхідно провести 43 досліду.
. Тоді N = 43, отже, для рішення поставленої задачі необхідно провести 43 досліду.
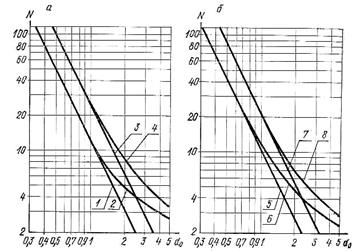
 Для ряду критеріїв побудовані графіки, що дозволяють за заданим значенням q, β і d0 визначити необхідний обсяг N вибірки. Зразки таких графіків (q = 0,05; β = 0,05), запозичені з [14], де маються також аналогічні графіки для q = 0,05; q = 0,01; β = 0,05; β = 0,10 ; β = 0,20; β = 0,50, представлені на рис. 3.7.
Для ряду критеріїв побудовані графіки, що дозволяють за заданим значенням q, β і d0 визначити необхідний обсяг N вибірки. Зразки таких графіків (q = 0,05; β = 0,05), запозичені з [14], де маються також аналогічні графіки для q = 0,05; q = 0,01; β = 0,05; β = 0,10 ; β = 0,20; β = 0,50, представлені на рис. 3.7.
Рисунок 3.7 - Графіки обсягів вибірки, необхідні для перевірки гіпотез щодо значень математичних очікувань
q = 0,05; β = 0,05; 1 – для критерію №1 табл. 3.2. 2 - для № 4; 3 - для № 18; 4 - для № 21; 5 - для № 2, 3; 6 - для № 5, 6; 7 - для № 19, 20; 8 - для № 22, 23. Для критеріїв № 1-6: 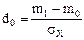 ; для критеріїв № 18-23:
; для критеріїв № 18-23: 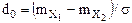 ;
; 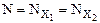
Відзначимо, що для критеріїв № 4-6 і № 21-23 відхилення d0 виражаються стосовно σ, хоча вона невідома. Як правило, необхідність завдання d0 у відносних одиницях не є серйозним обмеженням застосовності даної методики визначень необхідного обсягу вибірки, оскільки найчастіше значення d0 задається виходячи з загальних розумінь про властивості досліджуваного об'єкта і ступеня мінливості випадкової величини. Якщо ж такий підхід виявляється незадовільним, для критеріїв № 4-6 існує інший метод визначення N шляхом завдання параметра 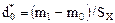 , де SХ обчислюється за результатами допоміжного експерименту з N* дослідів [14].
, де SХ обчислюється за результатами допоміжного експерименту з N* дослідів [14].
Графіки 1, 5 рис. 3.7 можна використовувати і для перебування N при перевірці гіпотез щодо значень коефіцієнта кореляції за допомогою критеріїв № 24–26. При цьому d0 = Zρ1–Zρ0, де ρ1 і ρ0 – конкуруючі значення коефіцієнта кореляції, а для визначення N треба до числа, знайденого за графіком, додати 3.
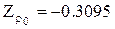 ;
; 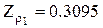 ;
; 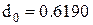 . Так як критерій, який варто тут використовувати, однобічний (№ 26 по табл. 3.2), то за допомогою графіка 5 рис. 3.7 знаходимо відповідне даному значенню d0 число: 26. Тоді N = 29.
. Так як критерій, який варто тут використовувати, однобічний (№ 26 по табл. 3.2), то за допомогою графіка 5 рис. 3.7 знаходимо відповідне даному значенню d0 число: 26. Тоді N = 29.
 Визначення необхідної кількості спостережень N для критеріїв № 7–12 і № 13–15 може вироблятися за допомогою таблиць так званих нецентральних
Визначення необхідної кількості спостережень N для критеріїв № 7–12 і № 13–15 може вироблятися за допомогою таблиць так званих нецентральних 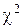 - і F-розподілів [9, 10], що, загалом, досить складно. Однак для найбільш розповсюджених на практиці ситуацій, коли використовуються однобічні критерії (№ 8, 9, 11, 12, 14, 15 по табл. 3.2), є прості формули, що дозволяють легко знайти N.
Якщо потрібно перевірити гіпотези Н0:
- і F-розподілів [9, 10], що, загалом, досить складно. Однак для найбільш розповсюджених на практиці ситуацій, коли використовуються однобічні критерії (№ 8, 9, 11, 12, 14, 15 по табл. 3.2), є прості формули, що дозволяють легко знайти N.
Якщо потрібно перевірити гіпотези Н0: 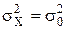 і Н1:
і Н1: 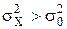 і при цьому з заданою надійністю розрізнити значення
і при цьому з заданою надійністю розрізнити значення 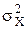 і
і 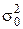 , причому
, причому 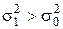 (
(  ), то необхідне число спостережень визначається в такий спосіб: за допомогою таблиці
), то необхідне число спостережень визначається в такий спосіб: за допомогою таблиці 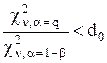 ;
; 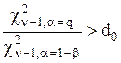 . (3.6)
Якщо ж необхідно розрізнити такі
. (3.6)
Якщо ж необхідно розрізнити такі 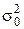 і
і 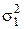 , що
, що 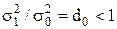 , то значення ν знаходиться аналогічним чином за допомогою співвідношень
, то значення ν знаходиться аналогічним чином за допомогою співвідношень
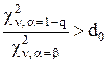 ;
; 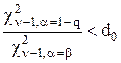 . (3.7)
В обох випадках N = ν для критеріїв № 8, 9 і N = ν +l для критеріїв № 11, 12.
. (3.7)
В обох випадках N = ν для критеріїв № 8, 9 і N = ν +l для критеріїв № 11, 12.
 Приклад 3.12. Провіряються гіпотези Н0:
Приклад 3.12. Провіряються гіпотези Н0: 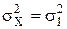 , де
, де 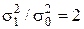 , то бажано, щоб гіпотеза Н0 була відкинута з ймовірністю 0,9 (тобто β = 0,1). Скільки спостережень повинно провестись для виконання цієї задачі?
Послідовно перебираючи з допомогою таблиці
, то бажано, щоб гіпотеза Н0 була відкинута з ймовірністю 0,9 (тобто β = 0,1). Скільки спостережень повинно провестись для виконання цієї задачі?
Послідовно перебираючи з допомогою таблиці 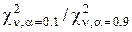 , переконуємось, що при
, переконуємось, що при 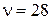 маємо
маємо 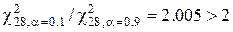 , а при
, а при 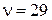
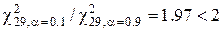 . Відповідно, нас задовільняє значення
. Відповідно, нас задовільняє значення 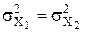 і Н1:
і Н1: 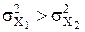 однобічним критерієм на рівні значимості q (випадок альтернативи
однобічним критерієм на рівні значимості q (випадок альтернативи 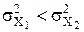 зводиться до розглянутого зміною індексів 1 і 2). Потрібно, щоб імовірність відхилення гіпотези, що перевіряється, була б щонайменше рівна 1 – β, як тільки
зводиться до розглянутого зміною індексів 1 і 2). Потрібно, щоб імовірність відхилення гіпотези, що перевіряється, була б щонайменше рівна 1 – β, як тільки 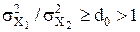 . Для виконання цієї вимоги необхідно використовувати вибірки обсягу
. Для виконання цієї вимоги необхідно використовувати вибірки обсягу 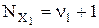 і
і 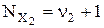 , де ν1 і ν2 знаходяться за допомогою наближеного співвідношення
, де ν1 і ν2 знаходяться за допомогою наближеного співвідношення
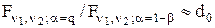 . (3.8)
Задача полегшується, якщо вибірки, по яких визначаються оцінки
. (3.8)
Задача полегшується, якщо вибірки, по яких визначаються оцінки 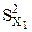 і
і 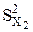 , однакового обсягу, тобто,
, однакового обсягу, тобто, 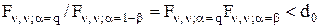 . (3.9.1)
. (3.9.1)
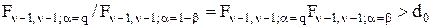 . (3.9.2)
Якщо до того ж q = β, умови (3.9) спрощуються ще більше:
. (3.9.2)
Якщо до того ж q = β, умови (3.9) спрощуються ще більше:
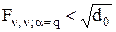 ; (3.10.1)
; (3.10.1)
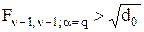 . (3.10.2)
. (3.10.2)
 Приклад 3.13. Дослідним шляхом порівнюється точність двох методів А і В, для чого проводиться N вимірів одного і того ж об’єкту обома методами [12].
С допомогою F-критерію провіряється гіпотеза про те, що точність методів однакова, тобто
Приклад 3.13. Дослідним шляхом порівнюється точність двох методів А і В, для чого проводиться N вимірів одного і того ж об’єкту обома методами [12].
С допомогою F-критерію провіряється гіпотеза про те, що точність методів однакова, тобто 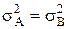 . Очікується, що метод А буде більш точним, і значить
. Очікується, що метод А буде більш точним, і значить 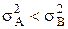 . Хоч метод В може бути менш точним, але він набагато простіший і швидший, і тому недоцільно вводити метод А, якщо його точність незначно перевищує точність методу В. Тому потрібно використати такий критерій, щоб ймовірність відхилення гіпотези
. Хоч метод В може бути менш точним, але він набагато простіший і швидший, і тому недоцільно вводити метод А, якщо його точність незначно перевищує точність методу В. Тому потрібно використати такий критерій, щоб ймовірність відхилення гіпотези 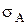 в 2 рази менше
в 2 рази менше 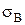 , вигода отримана від точності методу А, перекриє його негативні сторони. Тому необхідно, щоб в такій ситуації критерій встановив переваги метода А і відхилив гіпотезу
, вигода отримана від точності методу А, перекриє його негативні сторони. Тому необхідно, щоб в такій ситуації критерій встановив переваги метода А і відхилив гіпотезу  . Послідовно перебираючи різні табличні значення F-розподілу, отримуємо
. Послідовно перебираючи різні табличні значення F-розподілу, отримуємо 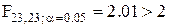 і
і 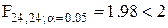 і в відповідності з умовами (3.10) знаходимо ν = 24. Відповідно, для того, щоб критерій задовольняв виставлені йому вимоги необхідно виконати кожним із методів 25 спостережень.
Формули (3.6) – (3.9) можна використовувати для наближеного визначення необхідного N у випадку двосторонніх критеріїв (№ 7, 10 і 13), якщо в цих формулах замість q скрізь записати q/2.
і в відповідності з умовами (3.10) знаходимо ν = 24. Відповідно, для того, щоб критерій задовольняв виставлені йому вимоги необхідно виконати кожним із методів 25 спостережень.
Формули (3.6) – (3.9) можна використовувати для наближеного визначення необхідного N у випадку двосторонніх критеріїв (№ 7, 10 і 13), якщо в цих формулах замість q скрізь записати q/2.