Геометрическое приложение определённого интеграла: вычисление площади фигуры и площади в полярных координат. Пример.

27.Вопрос

1 Площадь криволинейной трапеции.

Теорема: если фигура ограничена линиями f1(x), f2(x), x=a; x=b причём f1(x)≥0, f2(x)≤0 и f1(x)≤f2(x) для любых x принадлежащих [a; b] то Sф=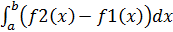

2 Площадь в полярных координатах.

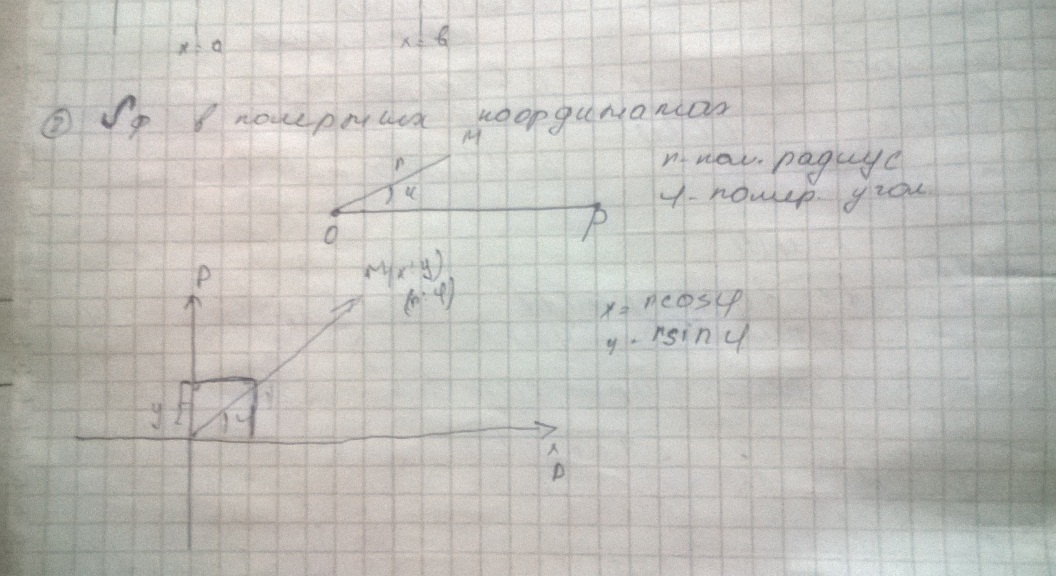
В полярной системе координат задаётся уравнение:

ɥ=f(u) sinuɥ=0

ɥ=2sinuɥ uɥ=πn

ɥ=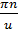

Фигура в декартовой системе координат.

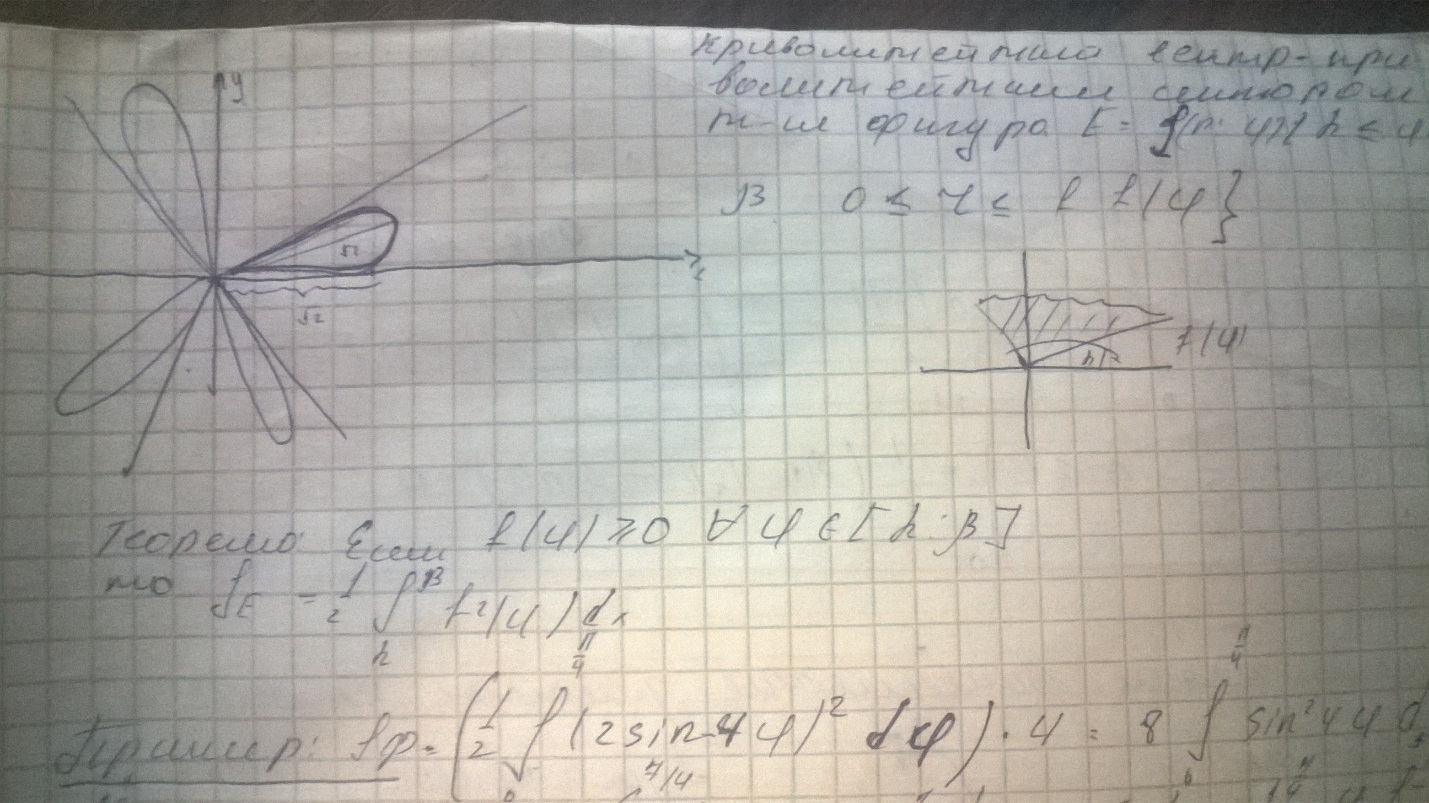
Теорема: Если f(ɥ)≥o для любого ɥ[α; β] то 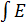= 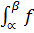^2(ɥ)dx