Хелпикс

Главная

Контакты

Случайная статья



Решения задач на вычисление площади фигуры.

Стр 1 из 2Следующая ⇒


Решения задач на вычисление площади фигуры.

Повторим формулы для вычисления площади с помощью интеграла:

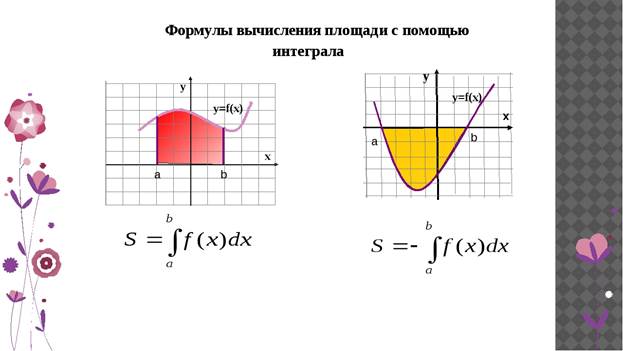
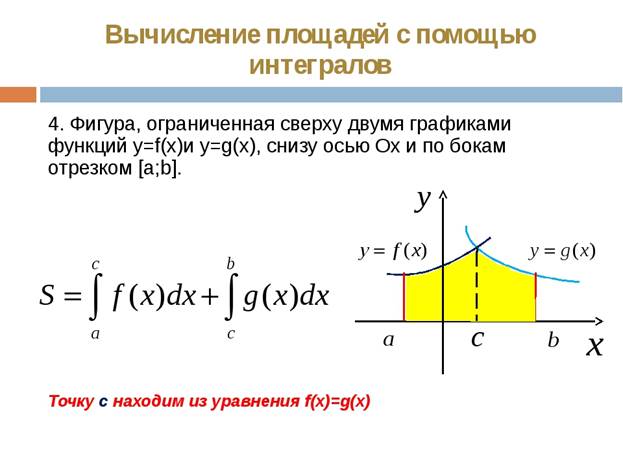
План решения задач на вычисление площади фигуры , ограниченной двумя функциями.

1 . Найти координаты точек (x;y) пересечения функций y=f(x) и y=g(x).

Для этого решить уравнение

f(x) = g(x)

2 . В прямоугольной системе координат ХОУ отметить данные точки. И провести через них графики заданных функций (если необходимо , то для построения графика найти точки пересечения его с осью ОХ(у=0))

3 . Выделить штриховкой фигуру, площадь которой необходимо найти.

4 . Выбрать формулу для вычисления площади фигуры.

5 . Сделать необходимые расчёты

Примеры решения задач

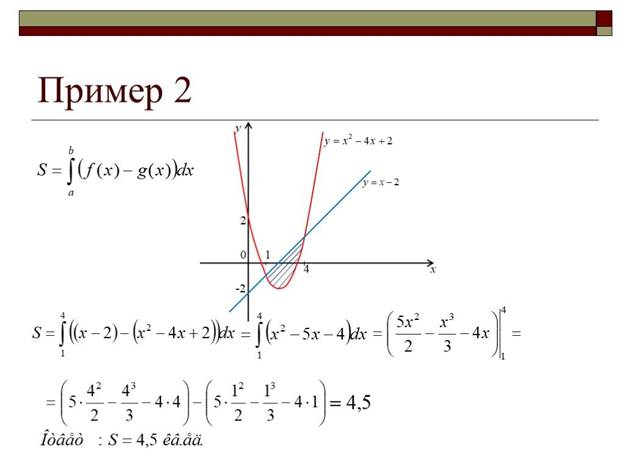
Пример 1. По рисунку записать формулу для вычисления площади изображённой фигуры

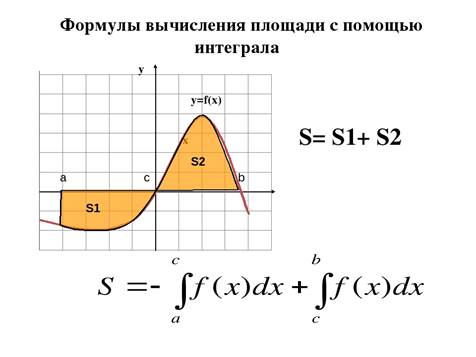
S= -  +

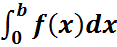
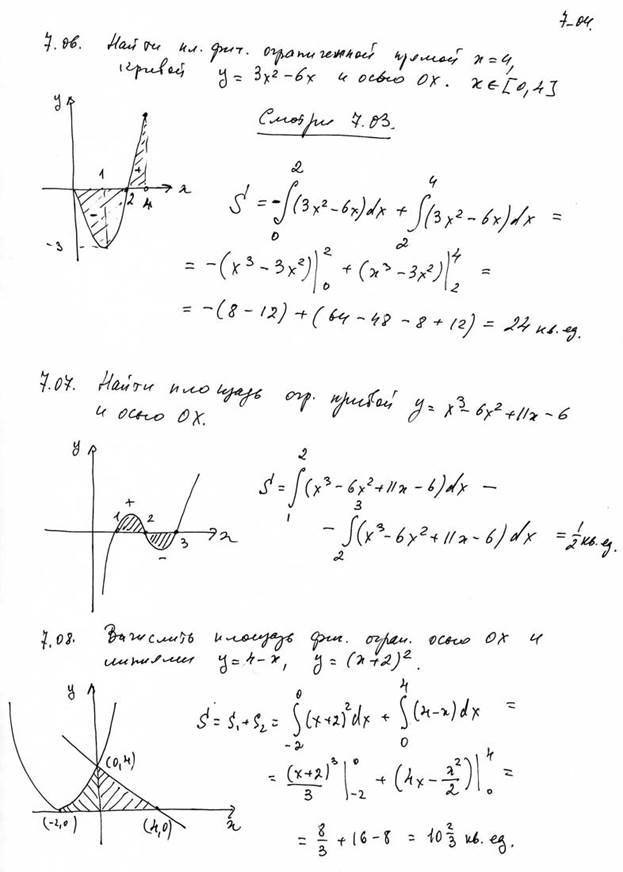
Задание на 20.05. РЕШИТЬ ЗАДАЧИ:   

Задание1: (Площади вычислять не надо)

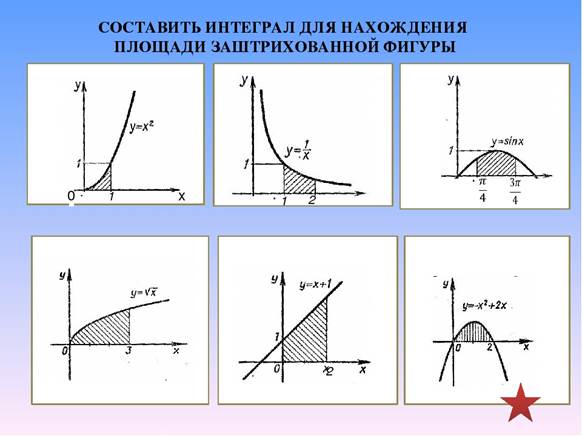
Задание 2:

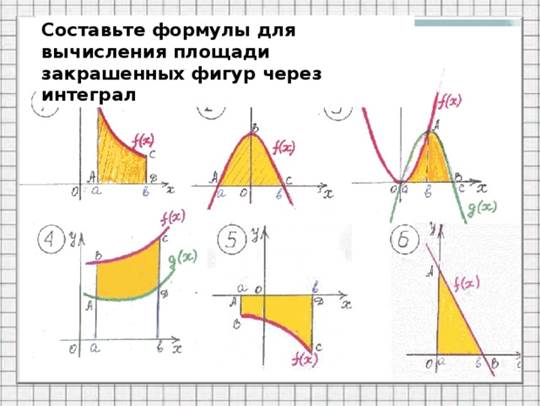
Задание 3:Записать по данному рисунку формулу для вычисления площади заштрихованной фигуры( интегралы вычислять не надо вычислять не надо)

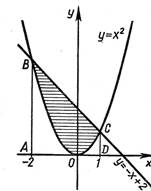
Задание 4:Найти ошибки в решении задачи и записать её правильное решение. 

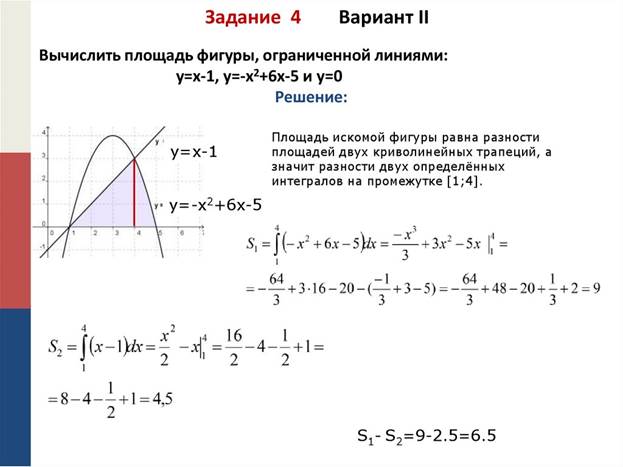
Начало решения задания 4:

1.Нахождение точек пересечения графиковпрямой у=Х-1и

Параболы у=-х2+6х-5:

Х-1= -х2+6х-5;

переносим всё в левую часть и приводим подобные слагаемые.

 х2-5х+4=0

Решаем квадратное уравнение и находим его корни х1=1 и х2= 4,

Тогда у1(1) =1-1=0 и у2(4)= 4-1=3.

2.Точки (1;0) и (4;3) строим в системе координат ХОУ и проводим через них прямую у= Х-1 и параболу у=-х2+6х-5.

4. Выделяем на рисунке фигуру, ограниченную прямой у=Х-1,


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.