Математика 16 группа урок 08.06.2020.

Математика 16 группа урок 08.06.2020.

Тема: Основные формулы тригонометрии.

Задание:

1. Изучить представленный материал.

2.Выписать все формулы, обязательно указать, как они называются.

3.Выполнить упражнения

ОСНОВНЫЕ ФОРМУЛЫ ТРИГОНОМЕТРИИ

Синус и косинус суммы и разности аргументов

№399. Представив 105⁰ как сумму 60⁰ + 45⁰, вычислите:

а) sin105° б) cos105°

№418. Используя формулы сложения, преобразуйте выражение:

а) sin(60° - β) б) cos(β — 30°)

№402. Вычислите:

а) sin74°cos16° + cos74°sin16°; б) cos23°cos22° - sin23°sin22°;

в) sin89°cos1° + cos89°sin1°; г) cos178°cos2° - sin178°sin2°.

№421.Найдите значение выражения:

а) cos107°cos17° + sin107°sin17°; б) cos36°cos24° - sin36°sin24°;

в) sin63°cos27° + cos63°sin27; б) sin51°cos21° - cos51°sin21°.

Упростите выражение:

а) sinхcos3х + cosхsin3х; б) cos2хcos5х — sin2хsin5х.

Формулы приведения

№158. Упростите выражение:

а) sin(90° - α) + cos(180° + α) + tg(270° + α) + ctg(360° +α);

б) sin(π/2 + t) - cos(π — t) + tg(π — t) + ctg(5π/2 — t).

№163. Вычислите: а) (11cos287° - 25sin557°) / sin17°.

№164.Вычислите: а) (2 cos11π/5 + 8 sin13π/10) / cosπ/5

Формулы двойного аргумента

Упростите выражение:

№462. а) sin2t / cost — sint; в) cos²t — cos2t.

№463. а) sin40° / sin20°; б) cos80° /(cos40° + sin40°).

Вычислите:

№55. а) sin(-π/4) + cos(π/3) + cos(-π/6); б) cos(π/6)∙cos(π/4)∙cos(π/3)∙cos(π/2);

в) sin(-π/4) — cos(-π) + sin(-3π/2); г) sin(π/6)∙sin(π/4)∙sin(π/3)∙sin(π/2).

№56. а) sin(-3π/4) + cos(-π/4) + sin(π/4)∙cos(π/2) + cos0∙sin(π/2);

б) cos(5π/3) + cos(4π/3) + sin(3π/2)∙sin(5π/8)∙cos(3π/2).

№59. Найдите наименьшее и наибольшее значения выражения:

а) 2sin t ; б) 3 + 4cos t ; в) -3cos t ; г) 3 – 5sin t .

Упростите выражение:

№60. а) 1 – sin² t ; б) 1 – cos² t ; в) 1 + sin² t + cos² t ; г) sin t - sin t ∙ cos² t .

№61. а) (sin t – cos t)² + 2 sin t ∙ cos t ; б) (sin t + cos t)² – 2 sin t ∙ cos t .

№73. а) sin² t /(1 + cos t) ; б) sin⁴ t + cos⁴ t + 2 sin² t ∙ cos² t ;

в) cos² t /(1 + sin t) + sin t ; г) cos⁴ t + cos² t ∙ sin² t - cos² t + 1.

Показываю решение примеров

sin74°cos16° + cos74°sin16° = sin (74° + 16°) = sin90° = 1.

(11cos287° - 25sin557°) / sin17° = =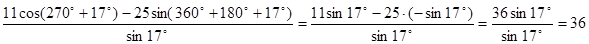

sin2t / cost — sint =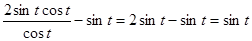

Остальное пробуйте сами, что осилите.