Во-вторых, свернуть схему относительно Е2 и выполнить аналогичные математические расчеты;

Сложная электрическая цепь – это цепь с несколькими источниками энергии, которую нельзя рассматривать как сочетание последовательного и параллельного соединений. Теоретической основой методов расчета и анализа сложных электрических цепей постоянного тока являются закон Ома и 1 и 2 законы Кирхгофа.

1. По МУ и КУ необходимо помнить, что уравнений должно быть столько, сколько и ветвей имеет сложная электрическая цепь.

- по первому закону Кирхгофа необходимо составить уравнений на одно меньше по сравнению с количеством узлов;

· если узлов два – одно уравнение;

· если узлов три – два уравнения; и т.д.

- по второму закону Кирхгофа уравнений составляется на одно меньше, чем контуров;

· n-1

· если контуров три – два уравнения;

· если контуров четыре – три уравнения; и т.д.

Методику расчетов по МУ и КУ необходимо соблюдать по Л-21.

2. При расчете сложной электрической цепи – 1 методом контурных токов (МКТ) необходимо соблюдать:

- по первому закону Кирхгофа уравнения не составляются;

n-1(уравнений на одно меньше числа контуров);

Методика расчетов МКТ должна соблюдаться в соответствии с Л-22.

3. При расчете сложных электрических цепей – 1 методом наложения токов необходимо соблюдать определенные этапы:

Во-первых, свернуть схему относительно Е1 и рассчитать ЕЕКВ (эквивалентное сопротивление); токи которые называются частичными, определить по закону Ома; определить узловое напряжение;

Во-вторых, свернуть схему относительно Е2 и выполнить аналогичные математические расчеты;

В-третьих, наложить одну схему на другую и в конечном итоге определить действующие токи и проверить правильность решения задачи первым законом Кирхгофа;

Методика расчета проводиться с соблюдением рекомендации по Л-23.

4. Методика эквивалентного генератора (МЭГ) применяется в случае, когда одна из ветвей сложной электрической цепи имеет меняющееся сопротивление, и задача заключается в определении тока в этой ветви при разных значениях сопротивления.

Определяются: проводимости ветвей R_ЕКВ, E_ЕКВ и ток в ветви с переменным сопротивлением. Затем строится график зависимости

I = f(R)

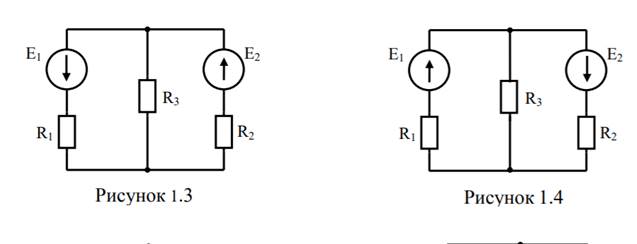
Метод наложения применяется для расчета электрических цепей, имеющих несколько э. д. с. Сущность метода наложения состоит в том, что ток в какой-либо части цепи можно считать состоящим из ряда частичных токов, вызванных каждой отдельной э. д. с, причем остальные э. д. с. принимаются равными нулю.

Рассмотрим пример.

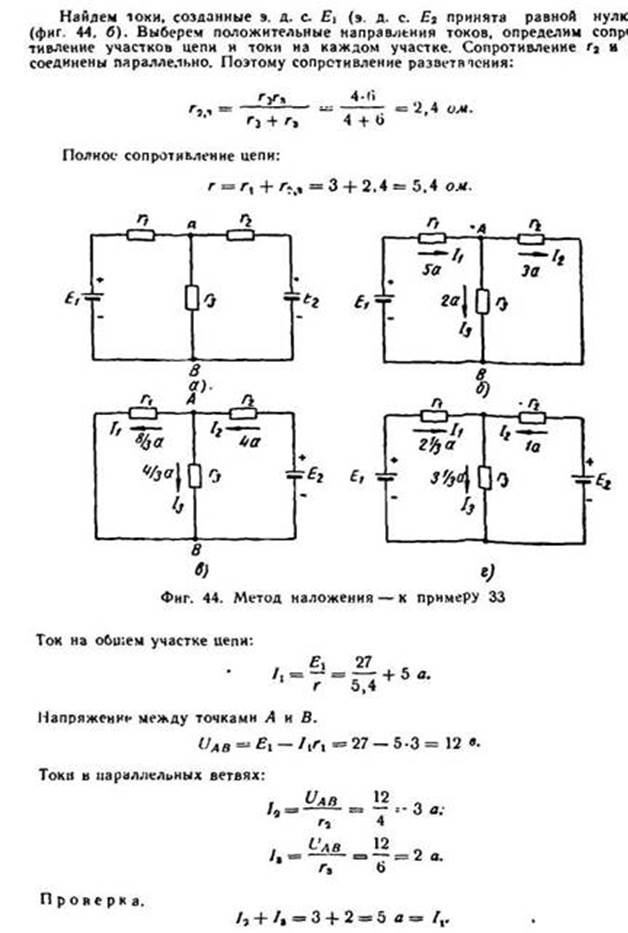
Пример 33 (фиг. 44, а). Дано E₁=27 в, E₂=24 в, r₁=3 ом, r₂=4 ом, r₃=6 ом. Определить, как распределяются токи в цепи.