Цикл с переменной. Вложенные циклы

Цикл с переменной

В информатике важную роль играют степени числа 2 (2, 4, 8, 16 и т.д.) Чтобы вывести все степени двойки от 21 до 210 мы уже можем написать такую программу с циклом «пока»:

k = 1;

n = 2;

while ( k <= 10 )

{ cout << n << endl;

n = n * 2;

k ++; }

Вы наверняка заметили, что переменная k используется трижды: в операторе присваивания начального значения, в условии цикла и в теле цикла (увеличение на 1). Чтобы собрать все действия с ней в один оператор, во многие языки программирования введен особый вид цикла – цикл с переменной. В заголовке этого цикла задается начальное значение этой переменной, условие продолжения цикла и изменение переменной в конце каждого шага цикла:

n = 2;

for ( k = 1; k <= 10; k++)

{ cout << n << endl;

n *= 2; }

С каждым шагом цикла переменная цикла может не только увеличиваться, но и уменьшаться. Следующая программа печатает квадраты натуральных чисел от 10 до 1 в порядке убывания:

for ( k = 10; k >= 1; k-- )

cout << k*k << endl;

Шаг изменения переменной цикла может быть любым числом. Например, следующий цикл выводит квадраты нечётных чисел:

for ( k = 1; k <= 10; k+=2 )

cout << k*k << endl;

Вложенные циклы

В более сложных задачах часто бывает так, что на каждом шаге цикла нужно выполнять обработку данных, которая также представляет собой циклический алгоритм. В этом случае получается конструкция «цикл в цикле» или «вложенный цикл».

Предположим, что нужно найти все простые числа в интервале от 2 до 1000. Простейший (но не самый быстрый) алгоритм решения такой задачи на псевдокоде выглядит так: сделать для n от 1 до 1000 если число n простое то вывод n Как же определить, что число простое? Как известно, простое число делится только на 1 и само на себя. Если число n не имеет делителей в диапазоне от 2 до n-1, то оно простое, а если хотя бы один делитель в этом интервале найден, то составное. Чтобы проверить делимость числа n на некоторое число k, нужно взять остаток от деления n на k. Если этот остаток равен нулю, то n делится на k.

Таким образом, программу можно записать так (здесь n, k и count – целочисленные переменные, count обозначает счётчик делителей):

for (n = 2; n <= 1000; n ++)

{ count= 0;

for ( k = 2; k < n; k ++ )

if ( n % k == 0 )

count ++;

if ( count == 0 )

cout << n << endl; }

Попробуем немного ускорить работу программы. Делители числа обязательно идут в парах, причём в любой паре меньший из делителей не превосходит √n (иначе получается, что произведение двух делителей, каждый из которых больше √n , будет больше, чем n). Поэтому внутренний цикл можно выполнять только до значения √n вместо n-1. Для того, чтобы работать только с целыми числами (и таким образом избежать вычислительных ошибок), лучше заменить условие k ≤ √n на равносильное ему условие k² ≤ n. При этом потребуется перейти к внутреннему циклу с условием:

count = 0;

k = 2;

while ( k*k <= n )

{ if ( n % k == 0 )

count ++;

k ++; }

Чтобы еще ускорить работу цикла, заметим, что когда найден хотя бы один делитель, число уже заведомо составное, и искать другие делители в данной задаче не требуется. Поэтому можно закончить цикл. Для этого в условие работы цикла добавляется условие n % k != 0, связанное с имеющимся условием с помощью операции «И», при этом можно обойтись без переменной count:

k = 2;

while ( k*k <= n && n % k != 0 )

k ++;

if ( k*k > n )

printf("%d\n", n);

После выхода из цикла мы проверяем, какое условие было нарушено. Если k*k>n (нарушено первое условие в заголовке цикла), то число n простое. В любом вложенном цикле переменная внутреннего цикла изменяется быстрее, чем переменная внешнего цикла. Рассмотрим такой вложенный цикл:

for ( i = 1; i <= 4; i++ )

{ for ( k = 1; k <= i; k++ )

{ ... } }

На первом шаге (при i=1) переменная k принимает единственное значение 1. Далее, при i=2 переменная k принимает последовательно значения 1 и 2. На следующем шаге при i=3 переменная k проходит значения 1, 2 и 3, и т.д.

Порядок действий:

1. Разработать блок-схемы задач согласно варианту

2. Написать программный код по задачам согласно варианту

3. Составить отчет

4. Защита отчета

Задачи:

1. Мишина – 12, 32

2. Цыбанев – 17, 34

3. Склеменова – 16, 33

4. Медведева – 15, 28

5. Шмарина – 11, 29

6. Золотарева – 6, 31

7. Якубов – 14, 30

8. Карпова – 7, 27

9. Попова – 4, 24

10. Петора – 2, 19

11. Рудюк – 13, 20

12. Богданова – 5, 21

13. Лабзин – 10, 25

14. Кулакова – 9, 18

15. Железникова – 3, 26

16. Кравченко – 8, 23

Чехранова – 1, 22

1. Заполнить двумерный массив случайными числами от 10 до 100. Посчитать сумму элементов отдельно в каждой строке и определить номер строки, в которой эта сумма максимальна.

2. Напишите программу, которая вводит два целых числа и находит их произведение, не используя операцию умножения. Учтите, что числа могут быть отрицательными.

3. Напишите программу, которая вводит натуральное число N и находит сумму всех натуральных чисел от 1 до N. Используйте сначала цикл с условием, а потом – цикл с переменной.

4. Напишите программу, которая вводит натуральное число N и выводит первые N чётных натуральных чисел.

5. Напишите программу, которая вводит натуральные числа a и b, и выводит квадраты натуральных чисел в интервале от a до b. Например, если ввести 4 и 5, программа должна вывести 4*4=16 5*5=25

6. Напишите программу, которая вводит натуральные числа a и b, и выводит сумму квадратов натуральных чисел в интервале от a до b.

7. Напишите программу, которая вводит натуральное число N и выводит на экран N псевдослучайных чисел. Запустите её несколько раз, объясните результаты опыта.

8. Напишите программу, которая строит последовательность из N случайных чисел на отрезке от 0 до 1 и определяет, сколько из них попадает в полуинтервалы [0; 0,25), [0,25; 0,5), [0,5; 0,75) и [0,75; 1). Сравните результаты, полученные при N = 10, 100, 1000, 10000.

9. Найдите все пятизначные числа, которые при делении на 133 дают в остатке 125, а при делении на 134 дают в остатке 111.

10. Напишите программу, которая вводит натуральное число N и выводит на экран все натуральные числа, не превосходящие N и делящиеся на каждую из своих цифр.

11. Числа Армстронга. Натуральное число называется числом Армстронга, если сумма цифр числа, возведенных в N-ную степень (где N – количество цифр в числе) равна самому числу. Например, 153 = 13 + 53 + 33 . Найдите все трёхзначные и четырёхзначные числа Армстронга.

12. Автоморфные числа. Натуральное число называется автоморфным, если оно равно последним цифрам своего квадрата. Например, 252 = 625. Напишите программу, которая вводит натуральное число N и выводит на экран все автоморфные числа, не превосходящие N.

13. Напишите программу, которая считает количество чётных цифр введённого числа.

14. Напишите программу, которая считает сумму цифр введённого числа.

15. Напишите программу, которая определяет, верно ли, что введённое число содержит две одинаковых цифры, стоящие рядом (как, например, 221).

16. Напишите программу, которая определяет, верно ли, что введённое число состоит из одинаковых цифр (как, например, 222).

17. *Напишите программу, которая определяет, верно ли, что введённое число содержит по крайней мере две одинаковых цифры, возможно, не стоящие рядом (как, например, 212).

18. Используя сначала цикл с условием, а потом – цикл с переменной, напишите программу, которая выводит на экран чётные степени числа 2 от 210 до 22 в порядке убывания.

19. Алгоритм Евклида для вычисления наибольшего общего делителя двух натуральных чисел, формулируется так: нужно заменять большее число на разность большего и меньшего до тех пор, пока одно из них не станет равно нулю; тогда второе и есть НОД. Напишите программу, которая реализует этот алгоритм. Какой цикл тут нужно использовать?

20. Напишите программу, использующую модифицированный алгоритм Евклида: нужно заменять большее число на остаток от деления большего на меньшее до тех пор, пока этот остаток не станет равен нулю; тогда второе число и есть НОД.

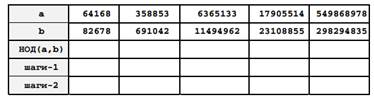
21. Добавьте в решение двух предыдущих задач вычисление количества шагов цикла. Заполните таблицу (шаги-1 и шаги-2 означают количество шагов двух версия алгоритма Евклида):

22. Напишите программу, которая вводит с клавиатуры 10 чисел и вычисляет их сумму и произведение.

23. Напишите программу, которая вводит с клавиатуры числа до тех пор, пока не будет введено число 0. В конце работы программы на экран выводится сумма и произведение введенных чисел (не считая 0).

24. Напишите программу, которая вводит с клавиатуры числа до тех пор, пока не будет введено число 0. В конце работы программы на экран выводится минимальное и максимальное из введенных чисел (не считая 0).

25. Напишите программу, которая вводит с клавиатуры натуральное число N и определяет его факториал, то есть произведение натуральных чисел от 1 до N: N!= 1⋅ 2⋅3⋅K⋅ N . Что будет, если ввести большое значение N (например, 20)?

26. Напишите программу, которая вводит натуральные числа A и N и вычисляет AN.

27. Напишите программу, которая выводит на экран все цифры числа, начиная с первой.

28. Ряд чисел Фибоначчи задается следующим образом: первые два числа равны 1 ( 1 F1 = F2 = ), а каждое следующее равно сумму двух предыдущих: Fn = Fn−1 + Fn−2 . Напишите программу, которая вводит натуральное число N и выводит на экран первые N чисел Фибоначчи.

29. Напишите программу, которая вводит натуральные числа a и b и выводит все простые числа в диапазоне от a до b. 30. Совершенным называется число, равное сумме всех своих делителей, меньших его самого (например, число 6=1+2+3).

30. Напишите программу, которая вводит натуральное число N и определяет, является ли число N совершенным.

31. Напишите программу, которая вводит натуральное число N и находит все совершенные числа в диапазоне от 1 до N.

32. В магазине продается мастика в ящиках по 15 кг, 17 кг, 21 кг. Как купить ровно 185 кг мастики, не вскрывая ящики? Сколькими способами можно это сделать?

33. *Ввести натуральное число N и вывести значение числа 1/N, выделив период дроби. Например, 1/2=0,5 или 1/7=0,(142857).

34. *В телевикторине участнику предлагают выбрать один из трёх закрытых чёрных ящиков, причём известно, что в одном из них – приз, а в двух других – пусто. После этого ведущий открывает один пустой ящик (но не тот, который выбрал участник) и предлагает заново сделать выбор, но уже между двумя оставшимися ящиками. Используя псевдослучайные числа, выполните моделирование 1000 раундов этой игры и определите, что выгоднее делать участнику викторины: выбрать тот же ящик, что и в начале игры, или другой.

⇐ Предыдущая 12