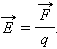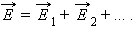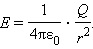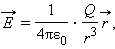- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Электрическое поле
Электрическое поле
По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.
Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не производит заметного перераспределения исследуемых зарядов.
Для количественного определения электрического поля вводится силовая характеристика 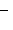 напряженность электрического поля.
напряженность электрического поля.
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:
|
Напряженность электрического поля – векторная физическая величина. Направление вектора Е в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.
Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим. Во многих случаях для краткости это поле обозначают общим термином – электрическое поле
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:
|
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции.
В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю
|
Это поле называется кулоновским. В кулоновском поле направление вектора Е зависит от знака заряда Q: если Q > 0, то вектор Е направлен по радиусу от заряда, если Q < 0, то вектор Е направлен к заряду.
Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r от заряда Q к точке наблюдения. Тогда при Q > 0 вектор E параллелен r, а при Q < 0 вектор E анти параллелен r. Следовательно, можно записать:
|
где r – модуль радиус-вектора r.
Вопрос 3:
Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт 1 В = 1 Дж/Кл
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
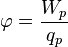
Напряжённость электростатического поля 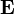 и потенциал
и потенциал 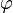 связаны соотношением[1]
связаны соотношением[1]
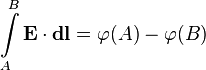
или обратно[2]:
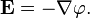
Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
— оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
4 Энергия системы зарядов
Найдем сначала выражение для потенциальной энергии системы двух точечных зарядов 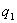 и
и 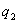 , находящихся на расстоянии
, находящихся на расстоянии 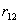 . Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние
. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние 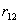 . При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая
. При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая 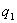 к
к 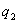 либо
либо 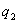 к
к 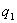 .Работа переноса заряда
.Работа переноса заряда 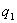 из бесконечности в точку, удаленную от
из бесконечности в точку, удаленную от 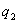 на
на 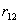
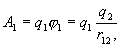
где 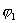 - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 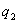 в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд 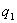 . Аналогично работа переноса заряда
. Аналогично работа переноса заряда 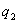 из бесконечности в точку, удаленную от
из бесконечности в точку, удаленную от 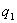 на
на 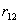 , равна
, равна
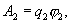
где 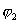 - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 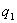 в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд 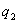 . Значение работ в обоих случаях одинаковы, и каждое из них выражает энергию системы
. Значение работ в обоих случаях одинаковы, и каждое из них выражает энергию системы
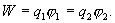
Для того чтобы в выражение энергии системы оба заряда входили симметрично, запишем его следующим образом:

Эта формула дает энергию системы двух зарядов. Перенесем из бесконечности еще один заряд 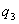 и поместим его в точку, находящуюся на расстоянии
и поместим его в точку, находящуюся на расстоянии 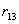 от
от 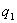 и
и 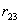 от
от 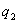 . При этом совершим работу
. При этом совершим работу
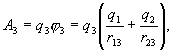
где 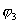 - потенциал, создаваемый зарядами
- потенциал, создаваемый зарядами 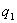 и
и 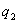 в той точке, в которую мы поместили заряд
в той точке, в которую мы поместили заряд 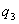 . В сумме с
. В сумме с 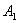 или
или 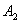 работа
работа 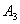 будет равна энергии трех зарядов:
будет равна энергии трех зарядов:
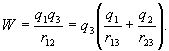
Последнее выражение можно привести к виду
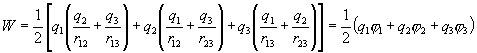
Добавляя к системе Зарядов последовательно 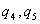 и т.д., можно убедиться в том, что в случае n зарядов потенциальная энергия системы равна
и т.д., можно убедиться в том, что в случае n зарядов потенциальная энергия системы равна
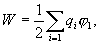
| (16.1) |
где 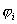 - потенциал, создаваемый в той точке, где находится
- потенциал, создаваемый в той точке, где находится 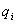 , всеми зарядами, кроме i-го.
, всеми зарядами, кроме i-го.
5 Связь между
Итак, электростатическое поле можно описать либо с помощью векторной величины 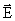 , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:
, либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:
Изобразим перемещение заряда q по произвольному пути l (Рис. 3.1) в электростатическом поле 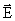 .
.
Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl, можно найти так:

| (3.4.1) |
где El – проекция 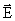 на
на 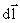 ; dl– произвольное направление перемещения заряда.
; dl– произвольное направление перемещения заряда.
С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl:
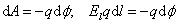 ,
,
отсюда
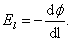
| (3.4.2) |
Для ориентации dl (направление перемещения) в пространстве, надо знать проекции 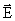 на оси координат:
на оси координат:
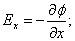
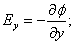
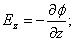
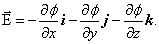
| (3.4.3) |
По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть
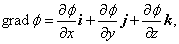
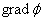 – вектор, показывающий направление наибыстрейшего увеличения функции.
– вектор, показывающий направление наибыстрейшего увеличения функции.
Тогда коротко связь между 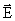 и φ записывается так:
и φ записывается так:
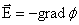
|
6 Поток вектора
В современной физике потоком вектора а называют скалярную физическую величину
Φа = ∫∫S а dS = ∫∫S (а n) dS , ( 1 )
где S – площадь произвольно расположенной поверхности;
а – произвольный вектор, начало которого лежит на поверхности S;
dS = n dS – псевдовектор, поставленный в соответствие ориентированной элементарной площадке (И.Бронштейн и К.Семендяев, 1968);
n – орт нормали к элементарной площадке dS.
Чаще всего приводится первая запись уравнения (1), но это не меняет того, что физическая величина Φа в уравнении (1) является скаляром. Псевдовектор элементарной площадки dS, является чистой математической абстракцией. В статье, посвященной физическому содержанию векторной величины, показано, что согласно принципу причинности произвольную векторную величину а следует рассматривать как локализациюполного вектора, распределенного по площади и приложенного в точке с заданными координатами.
Когда в математике и физике сначала вводят понятие частной величины (локального вектора), а затем – понятие общей величины, называемой потоком вектора, то мы имеем дело с не всегда оправданным применением индуктивного метода (от частного к общему). А дедуктивный метод (от общего к частному) предполагает сначала введение полной величины (неудачно названной в данном случае потоком вектора), а затем уже – введение локализованной величины (самого вектора).
Термин "поток вектора" является, по нашему мнению, отражением неаккуратности в присвоении названий физическим величинам и должен быть заменен другим термином. Процитируем популярный справочник по математике И.Бронштейна и К.Семендяева (1986): "Каждой ориентированной плоской площадке Σ можно поставить в соответствие вектор S, имеющий направление n и модуль, равный ее площади S ".
Приведем пример. На основании приведенной цитаты может показаться, что такая векторная величина, как перемещение объема ΔV, является скаляром, так как определяется скалярным произведением ΔV = хdS. Но приводимое в учебниках по физике указание на то, что "поток вектора скорости" является скалярной величиной, противоречит принципу причинности. Ведь перемещение x центра перемещаемого объема dVявляется следствием перемещения этого объёма, а не его причиной. При соблюдении принципа причинности следует записать выражение x = dV/dS. И тогда элементарная площадка dS остается скаляром, чем она, по сути дела, и является. А понятие о псевдовекторе площадки dS остается математической абстракцией, не имеющей физического содержания.
Почему же в теории физического поля применяются скалярные потоки вектора? Дело в том, что при анализе физического поля не применяются понятия о проточных системах и перемещаемых координатах состояния, и применение скалярных потоков вектора себя оправдывает теоретически, так как в этом случае оно не противоречит принципу причинности. Но и тут следует заметить, что вместо записи dS, как это принято в векторном анализе, предпочтительнее указывать запись ndS.
В частности, поток вектора магнитной индукции B (магнитный поток) Φm = ∫∫S BndS является величиной скалярной, ведь в магнитных цепях никакие энергоносители не перемещаются. Это следует объяснять при преподавании, чтобы не казалось, будто в магнитных цепях что-то движется. А такие мысли могут появиться по причине того, что в термине "магнитный поток" присутствует слово "поток".
. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности
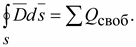 (15.11)
(15.11)
Вектор 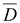 – это такая характеристика поля, которая не зависит от диэлектрических свойств среды.
– это такая характеристика поля, которая не зависит от диэлектрических свойств среды.
2. Так как 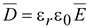 , то теорему Гаусса для однородной и изотропной среды можно записать:
, то теорему Гаусса для однородной и изотропной среды можно записать:
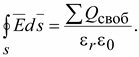 (15.12)
(15.12)
Вектор  – это характеристика поля, которая зависит от диэлектрических свойств среды.
– это характеристика поля, которая зависит от диэлектрических свойств среды.
3. Поток вектора  через любую замкнутую поверхность создается не только суммой свободных зарядов, но и суммой связанных зарядов
через любую замкнутую поверхность создается не только суммой свободных зарядов, но и суммой связанных зарядов
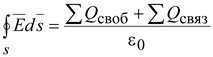 . (15.13)
. (15.13)
Теорему Гаусса можно использовать для нахождения напряженности или электрического смещения в какой-либо точке поля, если через эту точку можно провести замкнутую поверхность таким образом, что все ее точки будут в симметричных (одинаковых условиях по отношению к заряду, находящемуся внутри замкнутой поверхности).
Такой поверхностью являются обычно сфера (если заряд точечный), или боковая поверхность цилиндра (если заряд линейный).
| Теорема Остроградского-Гаусса |
Обозначим через G трехмерное тело, ограниченное кусочно-непрерывной, гладкой, замкнутой поверхностьюS с внешней нормалью. Предположим, что задано векторное поле
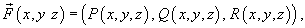 компоненты которого имеют непрерывные частные производные. Согласно формуле Остроградского-Гаусса,
компоненты которого имеют непрерывные частные производные. Согласно формуле Остроградского-Гаусса,
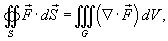 где через
где через
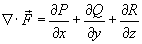 обозначена дивергенция векторного поля
обозначена дивергенция векторного поля 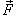 (она обозначается также символом (она обозначается также символом 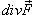 ). Символ ). Символ 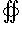 указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме: указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами. Данную формулу можно записать также в координатной форме:
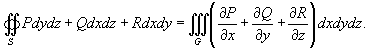 В частном случае, полагая
В частном случае, полагая 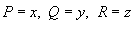 , получаем формулу для вычисления объема тела G: , получаем формулу для вычисления объема тела G:
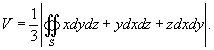
|
| Пример 1 |
Вычислить поверхностный интеграл 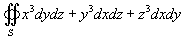 , где S − внешне ориентированная поверхность сферы, заданная уравнением , где S − внешне ориентированная поверхность сферы, заданная уравнением 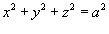 .
Решение.
Используя формулу Остроградского-Гаусса, можно записать .
Решение.
Используя формулу Остроградского-Гаусса, можно записать
 Вычислим полученный тройной интеграл в сферических интегралах.
Вычислим полученный тройной интеграл в сферических интегралах.
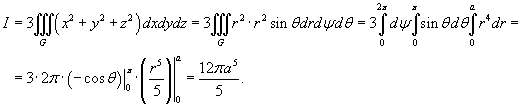
|
Теорема Гаусса выражает замечательное свойство электрического поля, которое позволяет представить эту теорему в иной форме, расширяющей ее возможности как инструмента исследования и расчета. Найдем дифференциальную форму теоремы Гаусса, в которой устанавливается связь между объемной плотностью заряда p иизменениями напряженности (E) в окрестности данной точки пространства.
Пусть имеем заряд q в объеме V, охватываемом замкнутой поверхностью S, представим его как
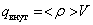 , ,
| (12.1) |
где < r> – среднее по объему V значение объемной плотности заряда. Запишем теорему Гаусса:
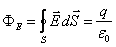 . .
| (12.2) |
Тогда подставим это выражение в (12.1) и разделим обе части равенства на V. В результате получим:
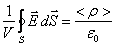 . .
| (12.3) |
Теперь устремим объем V®0, стягивая его к интересующей нас точке поля. Тогда <r> будет стремиться к значению r в данной точке поля, а левая часть уравнения будет стремиться к /0.
Величину, являющуюся пределом отношения 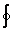 Е dSк V при V0, называют дивергенцией поляЕ и обозначают divE. То есть, по определению:
Е dSк V при V0, называют дивергенцией поляЕ и обозначают divE. То есть, по определению:
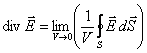 . .
| (12.4) |
Аналогично определяется дивергенция любого другого векторного поля. Из определения (12.4) следует, что дивергенция вектораEявляется скалярной функцией координат.
Чтобы найти дивергенцию Е надо взять бесконечно малый объем V, определить поток вектора Е сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Полученное выражение для дивергенции поля вектора Е будет зависеть от выбора системы координат (в разных системах координат оно оказывается разным). Если есть декартова система координат (x, y, z), то
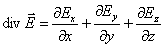 . .
| (12.5) |
Итак, мы выяснили, что при V0 в выражении (8.3) его правая часть стремится к /0, а левая – к divE. Из (12.4) следует, что дивергенция поля Е связана с плотностью заряда в той же точке уравнением:
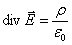 , ,
| (12.6) |
оно и выражает теорему Гаусса в дифференциальной форме.
В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда r в той же точке и больше ни от чего.
Написание многих формул и действия с ними значительно упрощаются, если ввести векторный дифференциальный оператор Ñ (набла, или оператор Гамильтона), Под этим вектором подразумевается вектор с компонентами /x, /y, /z. Следовательно, в декартовой системе координат оператор Ñ имеет вид:
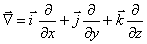 , ,
| (12.7) |
где i, j, k– орты осей x, y, z. Сам по себе вектор Ñ смысла не имеет. Он приобретает смысл только в сочетании со скалярной или векторной функцией, на которую он символически умножается. При умножении вектора набла на скаляр φ получим вектор – 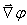 . Если умножим вектор Ñ скалярно на вектор Е, то получим скаляр:
. Если умножим вектор Ñ скалярно на вектор Е, то получим скаляр:
 , ,
| (12.8) |
а это и есть по определению не что иное, как divE или ÑЕ. То есть дивергенция поля E скаляр и может быть записана как divEили ÑЕ (в обоих случаях читается как – «дивергенция вектора Е»).
Если умножить вектор 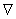 векторно на
векторно на 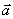 , то получится вектор с компонентами:
, то получится вектор с компонентами:
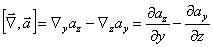 ,
,
которые совпадают с компонентами rot 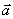 . Таким образом, существует два способа обозначений градиента, дивергенции и ротора:
. Таким образом, существует два способа обозначений градиента, дивергенции и ротора:
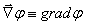 ;
;
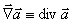 ;
;
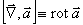 .
.
Обозначения с помощью оператора 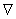 обладают рядом преимуществ, поэтому мы в дальнейшем и будем применять их. Например,
обладают рядом преимуществ, поэтому мы в дальнейшем и будем применять их. Например,
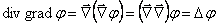 , ,
| (12.9) |
где Δ –оператор Лапласа;
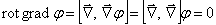 , ,
| (12.10) |
(векторное произведение вектора самого на себя равно нулю);
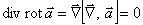 , ,
| (12.11) |
(смешанное произведение векторов равно объёму параллелепипеда, построенного на перемножаемых векторах как на сторонах, если два из этих векторов совпадают, объём параллелепипеда равен нулю).
Теорема Гаусса теперь может быть записана в виде:
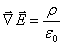 , ,
| (12.12) |
еще одна форма записи в дифференциальной форме теоремы Гаусса для электростатического поля в вакууме.
Дифференциальная форма записи электростатической теоремы Гаусса – это одно из замечательных свойств электрического поля. Т.е. в разных точках поля точечного заряда поле E отличается друг от друга, это же относится, вообще говоря, и к пространственным производным: Ex/x, Ey/y, Ez/z . Однако, по утверждению теоремы Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю. В тех точках поля, где div E>0 (дивергенция Е положительна), мы имеем источники поля (положительные заряды), а там где она отрицательна – стоки (отрицательные заряды).
Линии вектора Е выходят из источников поля, а заканчиваются в местах стоков.
Теорема Остроградского-Гаусса:
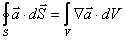 – это соотношение справедливо для любых векторных полей,
– это соотношение справедливо для любых векторных полей, 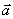 – векторная величина, характеризующая произвольное векторное поле.
– векторная величина, характеризующая произвольное векторное поле.

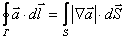 – теорема Стокса:
– теорема Стокса:
Циркуляция вектора 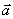 по произвольному замкнутому контуру Г равна потоку вектора rot
по произвольному замкнутому контуру Г равна потоку вектора rot 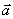 через произвольную поверхность S, ограниченную данным контуром.
через произвольную поверхность S, ограниченную данным контуром.
Она позволяет найти циркуляцию вектора 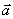 по контуру Г, ограничивающему поверхность S (контур может быть не плоским), если известен ротор вектора
по контуру Г, ограничивающему поверхность S (контур может быть не плоским), если известен ротор вектора 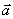 в каждой точке некоторой (не обязательно плоской) поверхности S.
в каждой точке некоторой (не обязательно плоской) поверхности S.
Рассмотрим несколько интересных на наш взгляд примеров расчета напряженности или разности потенциалов для электростатического поля.
10 поляризация
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.
Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
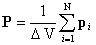 ,
,
где N - число молекул в объеме 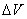 .
.
В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).
Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля
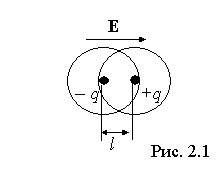
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля 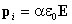 , где
, где 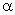 - поляризуемость молекулы. Значение поляризованности в этом случае равно
- поляризуемость молекулы. Значение поляризованности в этом случае равно 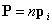 , где n - концентрация молекул
, где n - концентрация молекул 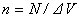 ;
; 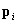 - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
- индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.
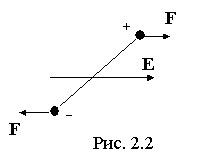
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.
Такая поляризация называется ориентационной. Поляризованность в этом случае равна 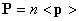 , где <p> - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
, где <p> - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как 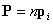 , где
, где 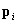 - значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.
- значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.

Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью 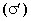 .
.
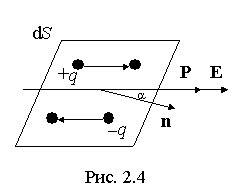
Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 2.4). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью 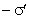 , а на другой положительные заряды с плотностью
, а на другой положительные заряды с плотностью 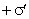 .
.
С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами 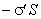 и
и 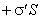 , которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен
, которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен 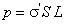 .
.
С другой стороны, электрический момент единицы объема равен 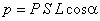 , где
, где 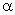 - угол, между направлением нормали к основанию призмы и вектором P. Произведение
- угол, между направлением нормали к основанию призмы и вектором P. Произведение 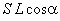 есть объем призмы.
есть объем призмы.
Приравняв друг к другу оба выражения для электрического момента, получаем, что поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации:
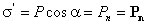 ,
,
где n - единичный вектор нормали к поверхности диэлектрика.
Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых 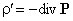 .
.
Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике
Из предыдущего раздела следует, что напряженность поля Е при переходе из вакуума в диэлектрик изменяется скачкообразно. Такой же эффект будет наблюдаться при переходе из одного диэлектрика в другой. Скачкообразное изменение вектора 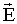 , обусловленное его зависимостью от e, затрудняет расчет полей при решении ряда задач. Поэтому для характеристики электрического поля целесообразно внести векторную величину
, обусловленное его зависимостью от e, затрудняет расчет полей при решении ряда задач. Поэтому для характеристики электрического поля целесообразно внести векторную величину 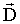 , которая не зависела бы от e. Этот вектор
, которая не зависела бы от e. Этот вектор 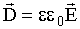 , он называется вектором электрического смещения или электрической индукции. Подставим в последнее соотношение e = 1+æ и получим
, он называется вектором электрического смещения или электрической индукции. Подставим в последнее соотношение e = 1+æ и получим
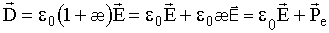 .
.
Обратимся вновь к рисунку 1.19. Внешнее поле  создается свободными зарядами заряженных поверхностей. Внутри диэлектрика действует также поле связанных зарядов, т.е. зарядов, входящих в состав атомов и молекул диэлектрика. Заряды, не связанные с перечисленными выше частицами диэлектрика, называют свободными. Это: а) заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электронов проводимости в металлах, электронов в вакууме, ионов в электролитах и т.п.); б) положительные заряды атомных остатков в металлах; в) избыточные заряды, сообщенные телу и нарушающие его электрическую нейтральность (например, заряды, нанесенные извне на поверхность диэлектрика).
создается свободными зарядами заряженных поверхностей. Внутри диэлектрика действует также поле связанных зарядов, т.е. зарядов, входящих в состав атомов и молекул диэлектрика. Заряды, не связанные с перечисленными выше частицами диэлектрика, называют свободными. Это: а) заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электронов проводимости в металлах, электронов в вакууме, ионов в электролитах и т.п.); б) положительные заряды атомных остатков в металлах; в) избыточные заряды, сообщенные телу и нарушающие его электрическую нейтральность (например, заряды, нанесенные извне на поверхность диэлектрика).
Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами. Первичным источником поля являются свободные заряды, а поле связанных зарядов возникает в результате поляризации диэлектрика при помещении его в поле свободных зарядов. Причем, поле связанных зарядов может вызвать перераспределение свободных зарядов и изменить поле этих зарядов.
Поэтому вектор 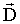 характеризует электростатическое поле, создаваемое свободными зарядами в вакууме (e=1), но при таком их распределении в пространстве, какое будет при наличии диэлектрика. Линии вектора
характеризует электростатическое поле, создаваемое свободными зарядами в вакууме (e=1), но при таком их распределении в пространстве, какое будет при наличии диэлектрика. Линии вектора 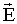 начинаются и заканчиваются на любых зарядах - свободных и связанных, а линии вектора
начинаются и заканчиваются на любых зарядах - свободных и связанных, а линии вектора 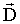 - только на свободных зарядах и они проходят диэлектрик не прерываясь. Смысл введения вектора электрического смещения состоит в том, что поток вектора
- только на свободных зарядах и они проходят диэлектрик не прерываясь. Смысл введения вектора электрического смещения состоит в том, что поток вектора 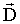 через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами, находящимися внутри объема, ограничивающего данную поверхность S (как это было с потоком
через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами, находящимися внутри объема, ограничивающего данную поверхность S (как это было с потоком 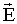 ). Это позволяет не рассматривать связанные (поляризованные) заряды и упрощает решение многих задач.
). Это позволяет не рассматривать связанные (поляризованные) заряды и упрощает решение многих задач.
Поток вектора 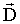 через произвольную замкнутую поверхность S равен
через произвольную замкнутую поверхность S равен 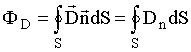 , где Dn - проекция вектора
, где Dn - проекция вектора 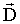 на нормаль
на нормаль 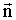 к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике выводится аналогично выводу теоремы для вакуума, в результате получаем
к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике выводится аналогично выводу теоремы для вакуума, в результате получаем 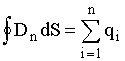 , где в правой части сумма свободных зарядов.
, где в правой части сумма свободных зарядов.
Исследуем связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (у которых диэлектрические проницаемости равны ε1 и ε2) при отсутствии на границе свободных зарядов.
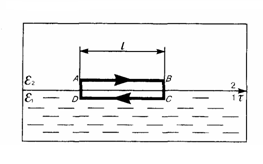
Рис.1
Проведем вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, с направлением ориентации, как показано на рис. 1. По теореме о циркуляции вектора Е, применительно к данному случаю
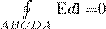
откуда
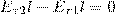
(знаки интегралов по АВ и CD разные, поскольку пути интегрирования противоположны, а интегралы по участкам ВС и DA малы). Поэтому
 (1)
(1)
Заменив проекции вектора Е проекциями вектора D, деленными на ε0ε, получим
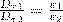 (2)
(2)
построим прямой цилиндр ничтожно малой высоты на границе раздела двух диэлектриков (рис. 2); одно основание цилиндра находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса для электростатического поля в диэлектрике
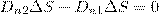
(нормали n и n' к основаниям цилиндра противоположно направлены). Поэтому
 (3)
(3)
Заменив проекции вектора D проекциями вектора Е, умноженными на ε0ε, получим
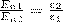 (4)
(4)
Значит, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е(Еτ) и нормальная составляющая вектора D(Dn) изменяются непрерывным образом (не испытывают скачка), а нормальная составляющая вектора Е(Еn) и тангенциальная составляющая вектора D(Dτ) испытывают скачок.
Из условий (1) — (4) для составляющих векторов Е и D мы видим, что линии этих векторов испытывают излом (преломляются). Найдем как связаны между углы α1 и α2 (на рис. 3 α1>α2). Используя (1) и (4), Еτ2 = Еτ1 и ε2En2 = ε1En1. Разложим векторы E1 и E2 на тангенциальные и нормальные составляющие у границы раздела. Из рис. 3 мы видим, что

Учитывая записанные выше условия, найдем закон преломления линий напряженности Е (а значит, и линий смещения D)
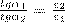
Из этой формулы можно сделать вывод, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали.
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|