
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача о двух балках
Для изображенной на Рис.1 расчетной схемы:
1. Записать дифференциальное уравнение нейтральной линии и определить прогиб балки 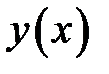 . Построить эпюры перерезывающих сил, моментов, углов поворотов и прогибов.
. Построить эпюры перерезывающих сил, моментов, углов поворотов и прогибов.
2. Определить аналитически, если это возможно, координату  , для которой прогиб достигает максимального значения по модулю.
, для которой прогиб достигает максимального значения по модулю.
3. В точке максимального прогиба  подкрепить конструкцию другой двухопорной балкой той же длины что и исходная так, чтобы минимизировать максимальное перемещение.
подкрепить конструкцию другой двухопорной балкой той же длины что и исходная так, чтобы минимизировать максимальное перемещение.
4. Записать дифференциальные уравнения упругой линии для системы балок. Определить прогибы  и
и 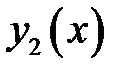 . Провести сравнение максимального прогиба для одной балки и системы балок. Сделать выводы.
. Провести сравнение максимального прогиба для одной балки и системы балок. Сделать выводы.
5. Провести расчет на прочность для исходной балки. С помощью полученных размеров сечения, определить максимальный прогиб в [мм] как для исходной расчетной схемы, так и для системы балок.
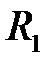
|
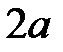
|
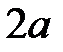
|
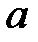
|
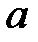
|
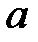
|

|
|
|
|
| Рис.1 |
|
|
|

|
|
|
Решение задачи:
Определим реакции в опорах  :
:
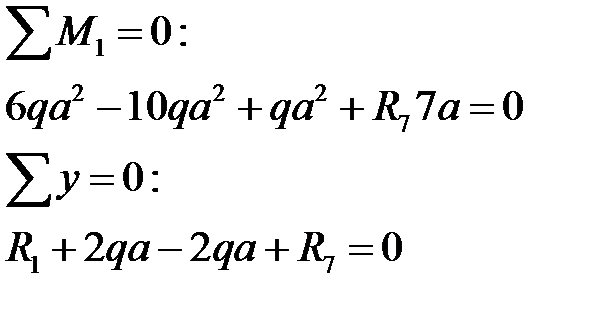
Решая систему, получим:
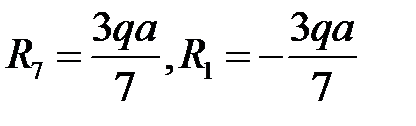
Далее будем записывать изгибающий момент 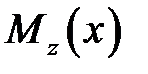 в системе координат, связанной с левым концом балки:
в системе координат, связанной с левым концом балки:
Участок 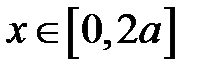 :
:
H Hiil5rnj/eLdUwD9TvLOKLx7oyD9B7yll0qj3/3TY/1+Xh5V3f9OePA/AAAA//8DAFBLAwQUAAYA CAAAACEAFHELseAAAAAKAQAADwAAAGRycy9kb3ducmV2LnhtbEyPQWuDQBCF74X+h2UKvTWrBk1j XEMIbU+h0KRQctvoRCXurLgbNf++01NzHN7Hm+9l68m0YsDeNZYUhLMABFJhy4YqBd+H95dXEM5r KnVrCRXc0ME6f3zIdFrakb5w2PtKcAm5VCuove9SKV1Ro9FuZjskzs62N9rz2Vey7PXI5aaVURAk 0uiG+EOtO9zWWFz2V6PgY9TjZh6+DbvLeXs7HuLPn12ISj0/TZsVCI+T/4fhT5/VIWenk71S6USr IIqTiFEOkgUIBuLlkrecOFnMA5B5Ju8n5L8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA 4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEA OP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA AVw0G2sJAADlMAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAA ACEAFHELseAAAAAKAQAADwAAAAAAAAAAAAAAAADFCwAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAE AAQA8wAAANIMAAAAAA== ">
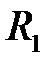
|
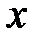
|
| Рис.2 |
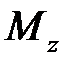
|
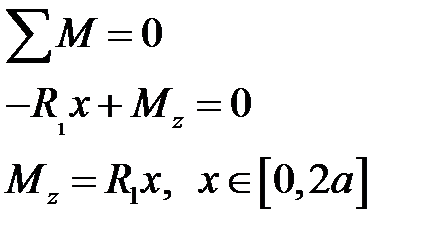
Участок 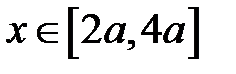 :
:
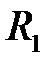
|
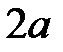
|

|
| Рис.3 |
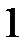
|
|
|
|
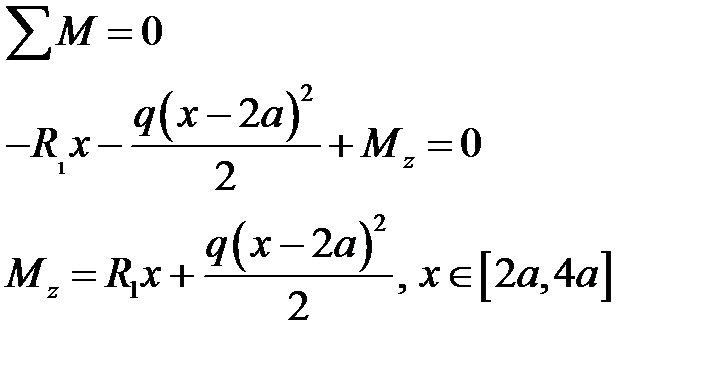
В выражении распределенная нагрузка засписана в предположении, что она ее область приложения при 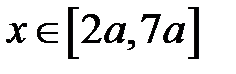 . Т.к. это не соответствует реальной расчетной схеме, на следующем участке
. Т.к. это не соответствует реальной расчетной схеме, на следующем участке 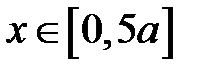 будем прикладывать дополнительную, компенсирующую силу:
будем прикладывать дополнительную, компенсирующую силу:
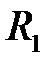
|
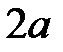
|
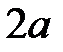
|

|
| Рис.4 |
|
|
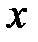
|
|

|

|
|
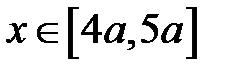 :
:
Для записи уравнений моментов на участке 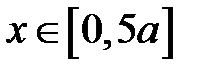 будем компенсировать несуществующую в исходной схеме на Рис.1 распределенную нагрузку (синий цвет) равной ей по величине (красной цвет).
будем компенсировать несуществующую в исходной схеме на Рис.1 распределенную нагрузку (синий цвет) равной ей по величине (красной цвет).
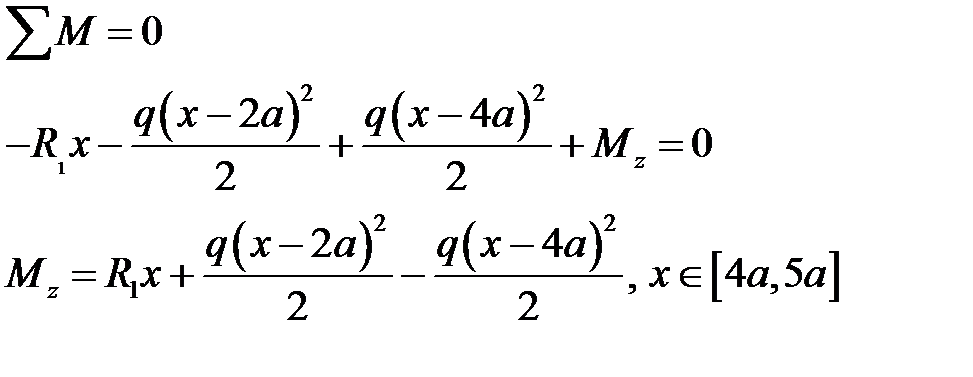
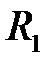
|
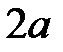
|
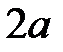
|

|
| Рис.5 |
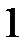
|
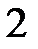
|
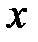
|
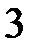
|

|

|
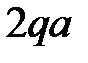
|
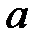
|
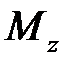
|
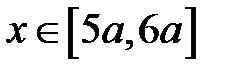 :
:
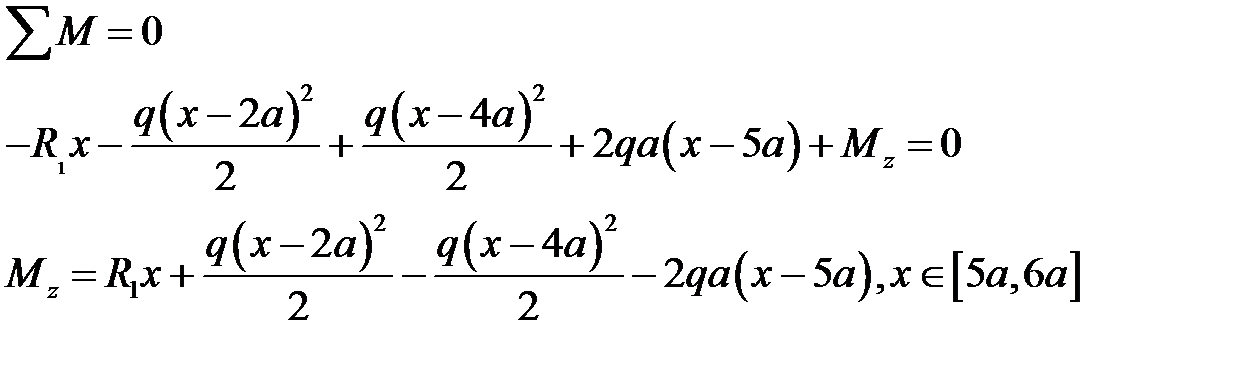
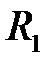
|
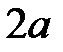
|
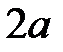
|

|
| Рис.6 |
|
|
|
|

|

|
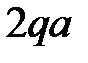
|
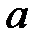
|
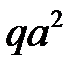
|
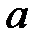
|
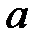
|
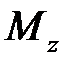
|
Участок 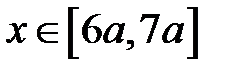 :
:

Формулы - позволяют записать изгибающий момент в виде:
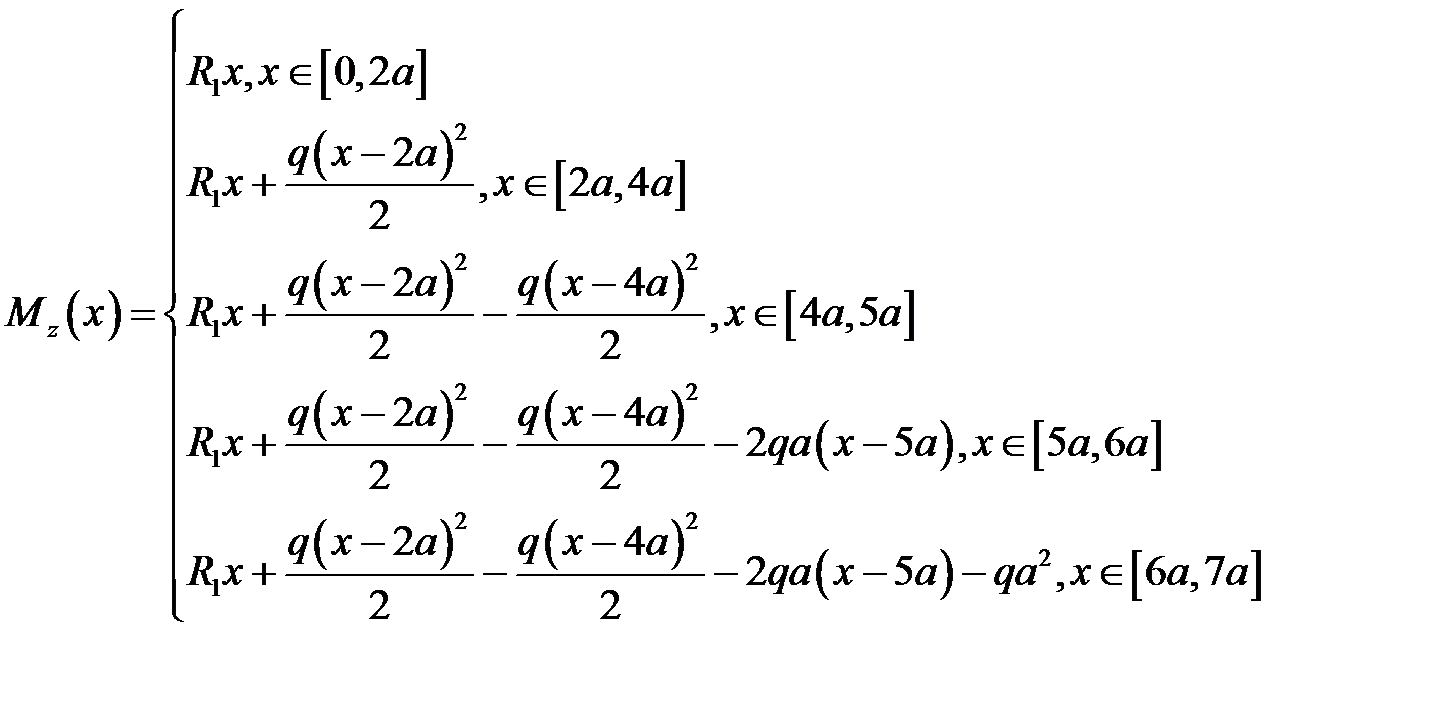
Эпюра моментов:
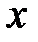
|
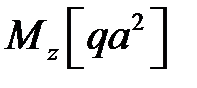
|
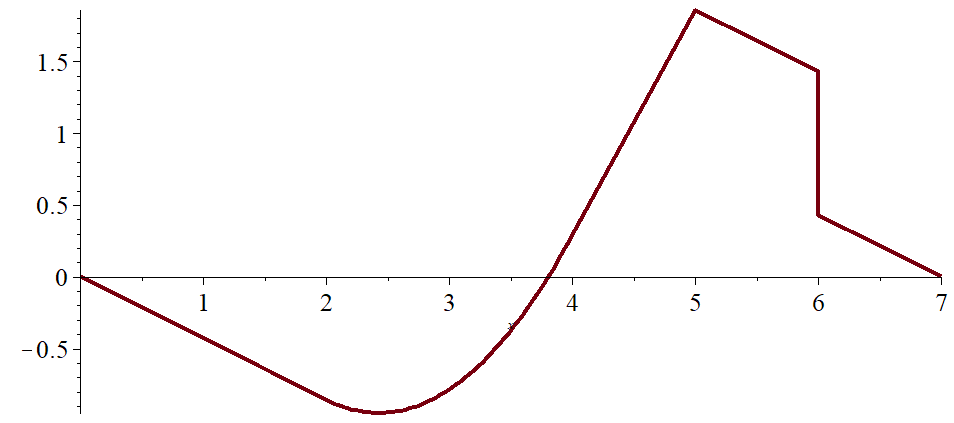
Запишем уравнение упругой линии балки:
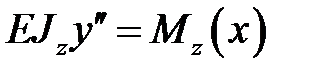
Проинтегрировав , получим угол поворота 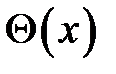 и прогиб
и прогиб 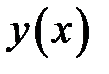 :
:
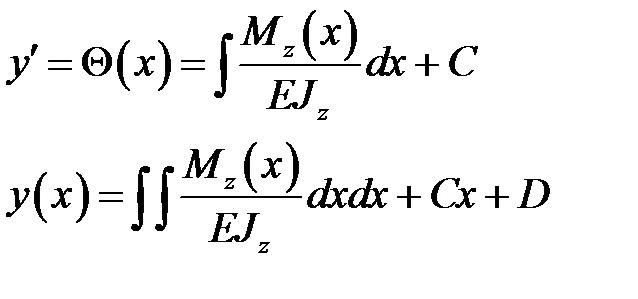
Константы инегрирования получим из условия закрепления балки:
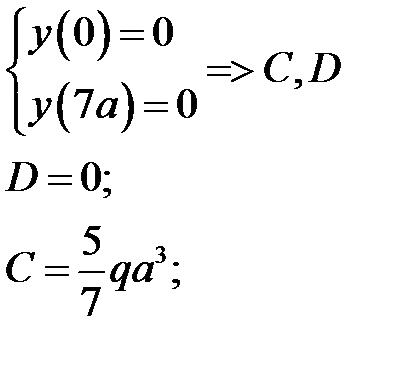
Изобразим упругую линию балки 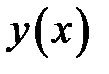 и угол поворота
и угол поворота 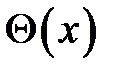 :
:
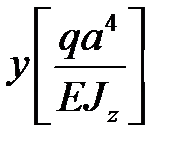
|
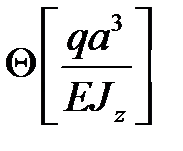
|
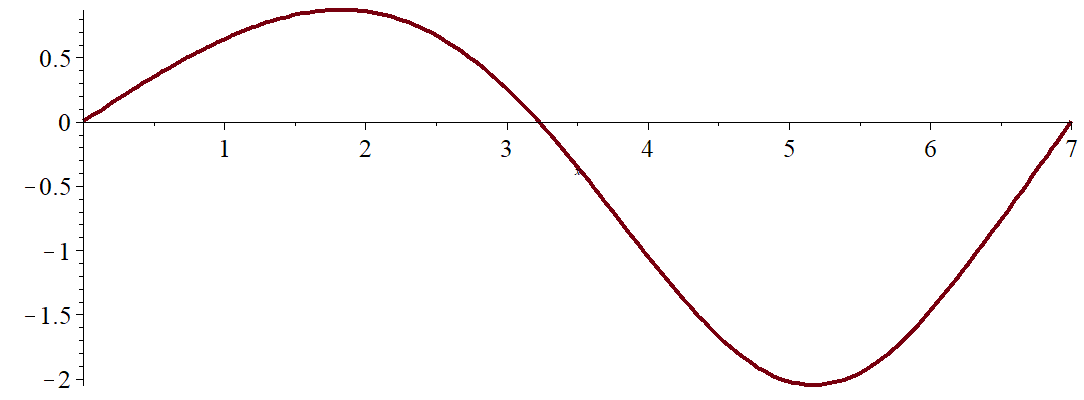
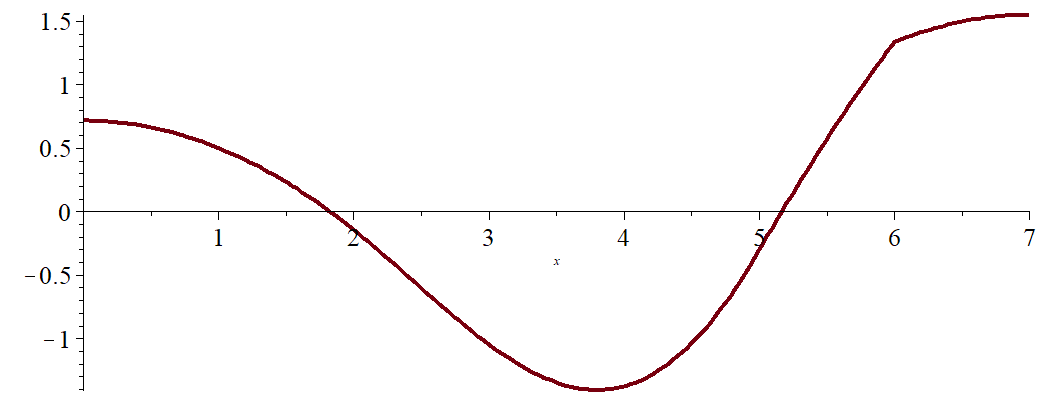
Из эпюры 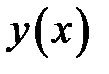 видно, что максимальный прогиб соответствует участку
видно, что максимальный прогиб соответствует участку 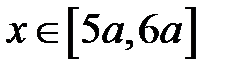 .
.
Определим координату максимального прогиба 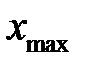 из условия:
из условия:
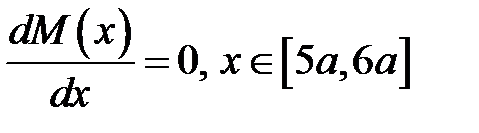
Из получаем  . Подставляя это значение в получаем значение максимального прогиба:
. Подставляя это значение в получаем значение максимального прогиба:  .
.
Задача о двух балках
Будем минимизировать максимальный прогиб в точке  путем подкрепления в рассматриваемой точке двухопорной балкой такой же длины. Жесткость второй балки в два раза превышает жесткость первой балки:
путем подкрепления в рассматриваемой точке двухопорной балкой такой же длины. Жесткость второй балки в два раза превышает жесткость первой балки: 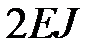 :
:
| Рис.2 |
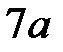
|
Будем предполагать, что балка «2» пересекается с первой балкой ровно посередине. Т.к. максимальные прогибы первой балки отрицательны, вторая балка будет расположена снизу:
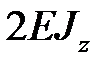
|
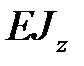
|
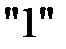
|

|
Данная задача приводится к системе двух балок со следующими расчетными схемами:
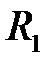
|
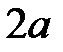
|
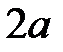
|
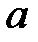
|
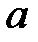
|
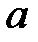
|

|
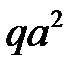
|
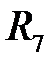
|
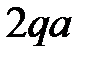
|
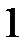
|
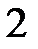
|
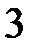
|

|
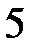
|
|
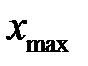
|
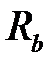
|
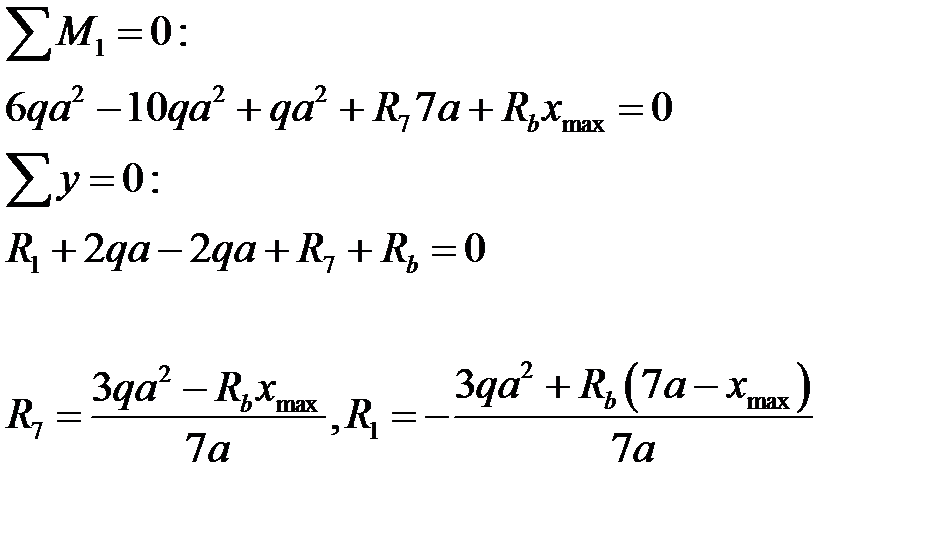
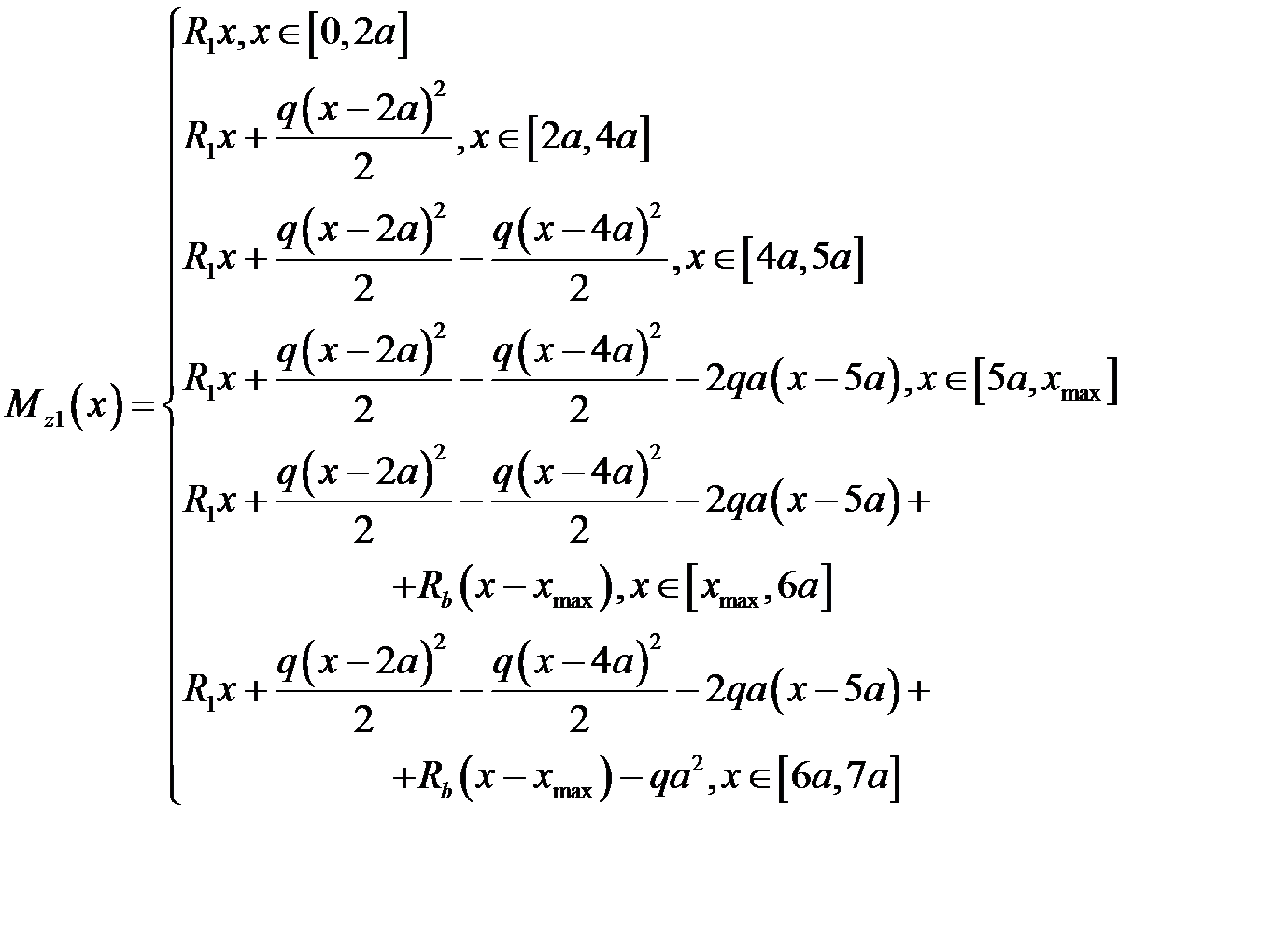
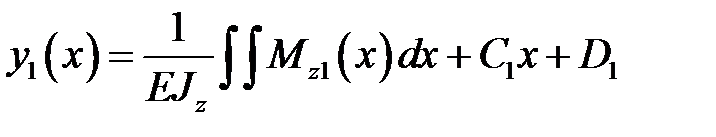
Рассмотрим балку «2»:
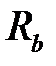
|

|

|

|
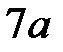
|
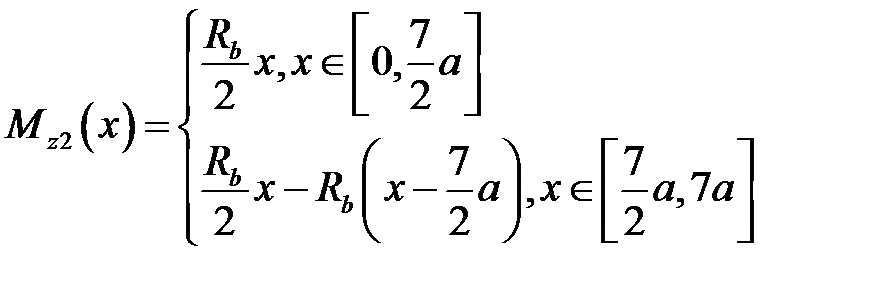
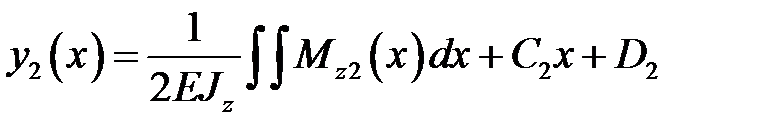

Из определим 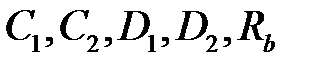 :
:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|