
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие
Практическое занятие
Марковские случайные процессы.
Для стохастических задач исследования редко удается построить математическую модель, позволяющую в явном виде найти интересующие величины в зависимости от условий операции α и элементов решения x. Но если процесс представляет собой, так называемый, марковский случайный процесс, то такая модель строится очень просто.
Вначале определим случайный процесс. Пусть имеется некоторая физическая система S, которая с течением времени меняет свое состояние,
причем заранее неизвестным случайным образом. Тогда говорят, что в системе S протекает случайный процесс. Пусть, например, система S – космический корабль, выводимый на заданную орбиту. Процесс вывода неизбежно сопровождается случайными ошибками, отклонениями от заданного режима, на который приходится вводить коррекцию, в которой нет необходимости при отсутствии ошибок. Значит процесс вывода на орбиту – случайный процесс. Практически все процесс в окружающем нас мире случайны. Но до тех пор, пока случайные возмущения системы несущественны, мало влияют на интересующие параметры, ими можно пренебрегать и рассматривать процесс как детерминированный и неслучайный. Необходимость учета случайностей возникает, когда они непосредственно касаются исследуемых параметров.
Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того когда и как система пришла в это состояние. Пусть в настоящий момент t0 система находится в определенном состоянии S0 (рис. 11). В данный момент времени t0 известно состояние системы и вся предыстория процесса. Все, что было при t < t0 . Если процесс случайный и непредсказуемый невозможно предсказать что произойдет с системой в будущем (t > t0). Но некоторые характеристики процесса можно определить, например, вероятность того, что через некоторое время τ останется система в состоянии S0 или перейдет в новое состояние S1.
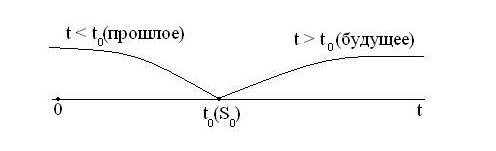
Рис. 11. Схема марковского процесса.
Если процесс марковский, то предсказывать можно, только учитывая настоящее состояние системы S0 и забыв о его предыстории. Само состояние S0, но как только оно достигнуто, о прошлом можно забыть, в марковском процессе «будущее зависит от прошлого только через настоящее».
Пример марковского процесса: система S – счетчик Гейгера, на который время от времени попадают космические частицы; состояние системы в момент времени t характеризуется показанием счетчика – число частиц, пришедшие до данного момента. Пусть в момент t0 счетчик показывает S0. Вероятность того, что в момент t > t0 счетчик покажет то или иное число частиц S1 зависит от t0, но не зависит от того, в какие именно моменты приходили частицы до момента t0.
Любой процесс можно рассматривать как марковский, если все параметры из прошлого от которого зависит будущее включить в настоящее. Например, имеется техническое устройство; в какойто момент t 0 оно еще исправно, необходимо определить вероятность того, что оно проработает еще время τ. Если за настоящее состояние системы считать просто «система исправна», то процесс не марковский, потому что вероятность того, что она не откажет за время τ, зависит от того, сколько времени она уже проработала и когда был последний ремонт. Если оба эти параметры (общее время работы и время после последнего ремонта) включить в настоящее состояние системы, то процесс можно будет считать марковским.
На практике марковские процессы в чистом виде практически не встречаются, но часто приходится иметь дело с процессами, для которых влиянием предыстории можно пренебречь. При изучении таких процессов можно с успехом применять марковские модели.
Классификация марковских случайных процессов производится в зависимости от непрерывности или дискретности множества значений
функции X(t) и параметра t. Различают следующие основные виды марковских случайных процессов:
– с дискретным состоянием и дискретным временем (цепь Маркова);
– с непрерывным состоянием и дискретным временем (марковские последовательности);
– с дискретным состоянием и непрерывным временем (непрерывная цепь Маркова);
– с непрерывным состоянием и непрерывным временем.
Марковские процессы с дискретными состояниями удобно представлять с помощью графа состояний (рис. 12), где состояния изображаются прямоугольниками (кругами и даже точками), а стрелками – возможные переходы из состояния в состояние. Возможные задержки в прежнем состоянии изображаются петлей. Число состояний системы может быть конечным и бесконечным (но счетным).
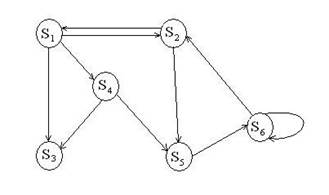
Рис. 12. Граф состояний системы.
Марковские процессы являются частным видом случайных процессов. Особое место марковских процессов среди других классов случайных процессов обусловлено следующими обстоятельствами: для марковских процессов хорошо разработан математический аппарат, позволяющий решать
многие практические задачи; с помощью марковских процессов можно описать поведение достаточно сложных систем.
Рассмотрим математический аппарат для марковских цепей. Для такого процесса моменты t1, t2, …, когда система S может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время , а номер шага 1, 2, 3, … k…. Случайный процесс в этом случае характеризуется посдедовательными
состояниями S(0), S(1), S(3), … S(k)… , где S(0) – начальное состояние системы (перед первым шагом), S(1) – состояние системы после первого шага, S(k) – состояние системы после k ого шага.
Последовательность состояний системы S(0), S(1), S(3), … S(k) (Sk) можно рассматривать как последовательность случайных событий. Такая случайная последовательность случайных событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния Si в любое состояние Sj не зависит от того, когда и как система пришла в состояние Si. Начальное состояние задается заранее или определяется случайно.
Вероятностями состояния цепи Маркова называются вероятности Pi(k) того, что после kго шага система S будет находиться в состоянии Si (i=1, 2, 3,… n). Очевидно для любого k
| n | |
| ∑Pi ( k )=1 | (25) |
| i=1 |
Начальным распределением вероятностей марковской цепи называется распределение вероятностей состояний в начале процесса:
P1(0) P2(0) ... Pi (0) ... Pn (0)
В частном случае, если начальное состояние системы S в точности известно Si(0)=Si, то начальная вероятность Pi(0)=1, а остальные вероятности равны нулю.
Вероятность перехода на kом шаге из состояния S i в состояние Sj называется условная вероятность того, что система S после kог о шага окажется в состоянии Sj при условии, что непосредственно перед этим она находилась в состоянии Si.
Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать n2 вероятностей перехода Pij, которые удобно представит в виде следующей матрицы:
P11
P21
...
 |  |  |  |
Pij =
Pi1
...
Pn1
| P12 | ... | P1n | |||
| P22 | ... | P2n | |||
| ... | ... | ... | |||
| (26) | |||||
| Pi 2 | ... | Pin | |||
| ... | ... | ... | |||
| P | ... | P | |||
| n 2 | nn | ||||
Матрица (2) называется матрицей переходных вероятностей или переходной матрицей. Если переходные вероятности не зависят от номера шага (от времени), и зависят только от того, из какого состояния и в какое совершается переход, то соответствующую цепь Маркова называют однородной. Переходные вероятности однородной марковской цепи образуют квадратную матрицу размером n × n. Отметим некоторые особенности этой матрицы:
1. Каждая строка характеризует выбранное состояние, и ее элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и переход в самое себя.
2. Элементы столбцов показывают вероятности всех возможных переходов системы за один шаг в заданное состояние (строка характеризует вероятность перехода из состояния, столбец – в состояние).
3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий.
| n | |
| ∑ Pij =1 i =1, n | (27) |

j =1
4. По главной диагонали матрицы переходных вероятностей стоят вероятности того, что система не выйдет из состояния Si, а останется в нем.
Если для однородной марковской цепи заданы начальное распределение вероятностей и матрица переходных вероятностей, то вероятность состояния системы Pi(k) (i=1,n; j=1,n) определяются по формуле:
| n | |
| Pi ( k )=∑Pj ( k −1) Pji (i =1, n j =1, n ) | (28) |


j=1
Пример. Рассмотрим процесс функционирования системы – автомобиль. Пусть автомобиль (система) в течение одной смены (суток )может находиться
в одном из двух состояний: исправном (S1) и неисправном (S2). Граф состояний представлен на рис. 13.
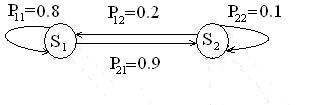
Рис. 13. Граф состояний автомобиля.
В результате проведения массовых наблюдений за работой автомобиля составлена следующая матрица вероятностей перехода:
0.8 0.2
 |  |  |
Pij =
0.9 0.1
где P11=0.8 – вероятность того, что автомобиль останется в исправном состоянии;
P12=0.2 – вероятность перехода автомобиля из состояния «исправен» всостояние «неисправен»;
P21=0.9 – вероятность перехода автомобиля из состояния «неисправен» всостояние «исправен»;
P22=0.1 – вероятность того, что автомобиль останется в неисправномсостоянии.
Вектор начальных вероятностей состояний автомобиля задан P1(0)=0,
P2(0)=1, P(0) = 1 .
Требуется определить вероятности состояний автомобиля через трое суток.
Используя матрицу переходных вероятностей, определим вероятности состояний Pi(k) после первого шага (первых суток).
| P1(1) | = P1 | (0)⋅ P11 | + P2(0)⋅ P21 | P1(1)=0⋅0.8+1⋅0.9=0.9 | |||
| P2(1) | = P1 | (0)⋅ P12 | + P2(0)⋅ P22 | P2(1)=0⋅0.2+1⋅0.1=0.1 | |||
| Вероятности | состояний | после второго шага (после вторых суток) | |||||
| P1(3) | = P1(2) | ⋅ P11 | + P2(2)⋅ P21 | P1(3)=0.81⋅0.8+0.19⋅0.9=0.819 | |||
| P2(3) | = P1(2) | ⋅ P12 | + P2(2)⋅ P22 | P2(3)=0.81⋅0.2+0.19⋅0.1=0.181 | |||
рассчитываются следующим образом:
Вероятности состояний после третьего шага (после третьих суток) равны:
| P1(2) | = P1(1)⋅ P11 | + P2(1)⋅ P21 | P1 | (2) = 0.9⋅0.8+ 0.1⋅0.9 = 0.81 |
| P2(2) | = P1(1)⋅ P12 | + P2(1)⋅ P22 | P2 | (2) = 0.9⋅0.2+ 0.1⋅0.1= 0.19 |
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы S из состояния в состояние происходят под действием какихто потоков событий (поток вызовов, поток отка зов, ноток восстановлений и т. д.). Если все потоки событий, переводящие систему S из состояния в состояние, — простейшие, то процесс, протекающий в системе,
будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем «будущее» не зависит от «прошлого».
Если система S находится в какомто состоянии Si, из которого есть непосредственный переход в другое состояние Sj (стрелка, ведущая из Si в Sj на графе состояний), то мы себе это будем представлять так, как будто на систему, пока она находится в состоянии Si, действует простейший поток событий, переводящий ее по стрелке Si → Sj. Как только появится первое со бытие этого потока, происходит «перескок» системы из Si в Sj.
Для наглядности очень удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Обозначим λij интенсивность потока событий, переводящего систему из состояния Si в Sj. На рис. 14,а дан граф состояний с проставленными у стрелок интенсивностями (мы будем называть такой граф
размеченным).
Построим размеченный граф состояний для системы (техническое устройство из двух узлов). Напомним состояния системы:
S0 — оба узла исправны,
S1 — первый узел ремонтируется, второй исправен,
S2 — второй узел ремонтируется, первый исправен,
Простейший характер потоков — достаточное, но не необходимое условие для того, чтобы процесс был марковским.
S3 — оба узла ремонтируются.
Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу.
а) б)
Рис. 14.Граф состояний системы.
Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии S0. Какой поток событий переводит ее в состояние S1? Очевидно, поток отказов первого узла. Его интенсивность λ1 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из S1 в S0? Очевидно, поток «окончаний ремонтов» первого узла. Его интенсивность 1 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 14, б.
Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система S, имеющая п возможных состояний S1, S2, ..., Sn. Назовем вероятностью iго состояния вероятность p i(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
| ∑n | p i ( t )=1 | (29) |
| i = |
Имея в своем распоряжений размеченный граф состояний, можно найти все вероятности состояний pi(t) как функции времени. Для этого составляются и решаются так называемые уравнения Колмогорова — особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.
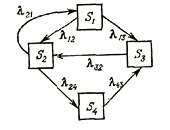
Рис. 15. Граф состояний системы.
Покажем на конкретном примере, как эти уравнения составляются. Пусть система S имеет четыре состояния: S1, S2, S3, S4, размеченный граф которых показан на рис. 15. Рассмотрим одну из вероятностей состояний, например p1(t). Это — вероятность того, что в момент t система будет в состоянии S1. Придадим t малое приращение ∆t и найдем p1(t+∆t) — вероятность того, что
в момент t+∆t система будет в состоянии S1. Как это может произойти? Очевидно, двумя способами: либо 1) в момент t система уже была в состоянии S1, а за время ∆t не вышла из него; либо 2) в момент t система была в состоянии S2, а за время ∆t перешла из него в S1. Найдем вероятность первого варианта. Вероятность того, что в момент t система была в состоянии S1, равна p1(t). Эту вероятность нужно умножить на вероятность того, что, находившись в момент t в состоянии S1, система за время ∆t не перейдет из него ни в S2, ни в S3. Суммарный поток событий, выводящий систему из состояния S1, тоже будет простейшим, с интенсивностью λ12 + λ13 (при наложении суперпозиции двух простейших потоков получается опять простейший поток, так как свойства стационарности, ординарности и отсутствия последействия сохраняются). Значит, вероятность того, что за время ∆t система выйдет из состояния S1, равна (λ12 + λ13) ∆t; вероятность
того, что не выйдет: 1–(λ12 + λ13) ∆t. Отсюда вероятность первого варианта равна p1(t) [1– (λ12 + λ13) ∆t].
Найдем вероятность второго варианта. Она равна вероятности того, что в момент t система будет в состоянии S2, а за время ∆t перейдет из него в
состояние S1, т, е. она равна p2 (t)λ21 t .
Складывая вероятности обоих вариантов (по правилу сложения
| вероятностей), получим: | |||
| p1(t + | t )= p1(t )[1−(λ12+ λ13) t ]+ p2(t )λ21 t | (30) | |
Раскроем квадратные скобки, перенесем p1(t) в левую часть и разделим обе части на ∆t:
в
| p1( t + t )− p1 | ( t ) | = λ21 p2 | ( t ) − ( λ12 | + λ13 ) p1 ( t ) | |
| t | |||||
| (31) | |||||
Устремим, как и полагается в подобных случаях, ∆t к нулю; слева получим в пределе производную функции p1(t). Таким образом, запишем дифференциальное уравнение для p1(t):
| dp1 | ( t ) | = λ21 p2 | ( t ) − ( λ12 | + λ13 ) p1 ( t ) | (32) | |
| dt | ||||||
или, короче, отбрасывая аргумент t у функций p1, p2 (теперь он нам больше уже не нужен):
| dp1 | = λ p −( λ + λ ) p | (33) | |||||
| dt | |||||||
Рассуждая аналогично для всех остальных состояний, напишем еще три дифференциальных уравнения. Присоединяя к ним уравнение (33), получим систему дифференциальных уравнений для вероятностей состояний:
| dp | = λ21 p2 | − ( λ12 + | λ13 ) p1 | ||||||||
|
|
|
| |||||||||
| dt | |||||||||||
|
| dp2 | = λ p + λ p −( λ + λ ) p | |||||||||
|
| |||||||||||
| dt | |||||||||||
| dp3 | |||||||||||
|
| = λ31 p1 + λ43 p4 − λ32 p3 | ||||||||||
|
| |||||||||||
| dt | |||||||||||
| dp | |||||||||||
|
| = λ24 p2 | − λ43 p4 | (34) | ||||||||
| dt | |||||||||||
Это — система четырех линейных дифференциальных уравнений с четырьмя неизвестными функциями p1, p2, p3, p4. Заметим, что одно из них (любое) можно отбросить, пользуясь тем, что p1+p2+p3+p4=1: выразить любую из вероятностей pi через другие, это выражение подставить в (34), а соответствующее уравнение с производной dpi отбросить.
в 
dt
Сформулируем теперь общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какогото ( iго) состояния. В правой части — сумма произведений вероятно стей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (1го) состояния.
в
Пользуясь этим правилом, запишем уравнения Колмогорова для системы S, размеченный граф состояний которой дан на рис. 15:
в
| dp | = µ1 p1 | + µ 2 p2−( λ1+ λ2) p0 | |||||||||||
|
|
| ||||||||||||
| dt | |||||||||||||
|
| dp1 |
|
| = λ p + µ p −( λ + µ ) p | |||||||||
| dt | |||||||||||||
| dp3 | |||||||||||||
|
|
| = λ2 p0+ µ 4 p3−( λ1+ µ2) p2 | |||||||||||
|
| |||||||||||||
| dt | |||||||||||||
| dp | |||||||||||||
|
| = λ2 p1 | + λ2 p2−( µ 2+ µ1) p3 | (35) | ||||||||||
| dt | |||||||||||||
Чтобы решить уравнения Колмогорова и найти вероятности состояний, прежде всего надо задать начальные условия. Если мы точно знаем начальное состояние системы Si, то в начальный момент (при t = 0) рi(0) = 1, а все остальные начальные вероятности равны нулю. Так, например, уравнения (35) естественно решать при начальных условиях р0(0) = 1, р1(0) = р2(0) = р3(0) =1 (в начальный момент оба узла исправны).
Как решать подобные уравнения? Вообще говоря, линейные дифференциальные уравнения с постоянными коэффициентами можно решать аналитически, но это удобно только, когда число уравнений не превосходит двух (иногда — трех). Если уравнений больше, обычно их решают численно — вручную или на ЭВМ. Таким образом, уравнения Колмогорова дают возможность найти все вероятности состояний как
функции времени.
Поставим теперь вопрос: что будет происходить с вероятностями состояний при t→∞? Будут ли р1(t), р2(t),… стремиться к каким-то пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний. В теории случайных процессов доказывается, что если число n состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют).
Предположим, что это условие выполнено и финальные вероятности существуют:
| lim pi (t ) = pi (i = 1, 2..., n ) | (36) |
| t→∞ |
Финальные вероятности мы будем обозначать теми же буквами р1, р2,..., что
и сами вероятности состояний, но разумея под ними уже не переменные величины (функции времени), а постоянные числа. Очевидно, они тоже образуют в сумме единицу:
| ∑n | p i ( t )=1 | (37) |
| i = |
Как понимать эти финальные вероятности? При t→∞ в системе S устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Финальную вероятность состояния Si, можно истолковать, как среднее относительное время пребывания системы в этом состоянии. Например, если система S имеет три состояния S1, S2, S3 и их финальные вероятности равны 0,2, 0,3 и 0,5, это значит, что в предельном, стационарном режиме система в среднем две десятых времени проводит в состоянии S1, три десятых — в состоянии S2, и половину времени — в состоянии S3.
Как же вычислить финальные вероятности? Очень просто. Если вероятности p1, p2,... постоянны, то их производные равны пулю. Значит, чтобы найти финальные вероятности, нужно все левые части в уравнениях Колмогорова положить равными нулю и решить полученную систему уже не дифференциальных, а линейных алгебраических уравнений. Можно и не писать уравнений Колмогорова, а прямо по графу состояний написать систему линейных алгебраических уравнений. Если перенести отрицатель ный член каждого уравнения из правой части в левую, то получим сразу систему уравнений, где слева стоит финальная вероятность данного состояния рi,,умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в iе состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пользуясь этим правилом, напишем линейные алгебраические уравнения для финальных вероятностей состояний системы, граф состояний которой дан на рис. 5.
( λ1 + λ2 ) p0 = µ1 p1 + µ2 p2
( λ + µ ) p = λ p + µ p
| ( µ | + µ ) p = λ p + λ p | (38) | |||||||
Эту систему четырех уравнений с четырьмя неизвестными p0, p1, p2, p3, казалось бы, вполне можно решить. Но уравнения (38) однородны (не имеют свободного члена) и, значит, определяют неизвестные только с точностью до произвольного множителя. К счастью, мы можем воспользоваться так на зываемым нормировочным условием:
| p0+ p1+ p2+ p3=1 | (39) |
и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить (оно вытекает как следствие из остальных).
Давайте зададимся численными значениями интенсивностей λ1=1,
λ2=2,
1=2, 3=3 и решим систему (14). Пожертвуем четвертым уравнением, добавив вместо него нормировочное условно (15). Уравнения примут вид:
| 3 p0 = 2 p1 +3p2 | ||
| 4 p1 = p0 +3p3 | ||
| 4 p2 =2 p0 +2p2 | ||
p0+ p1+ p2+ p3=1
Решая их, получим:




| p =6 | = 0,40; p = 3 | = 0,20; p = 4 | ≈ 0,27; p = 2 | ≈0,13; | |||||
т. е. в предельном, стационарном режиме система S в среднем 40% времени будет проводить в состоянии S0 (оба узла исправны), 20% —в состоянии S1
(первый узел ремонтируется, второй работает), 27% —в состоянии S2 (второй
узел ремонтируется, первый работает) и 13%—в состоянии S3 полной негодности (оба узла ремонтируются).
W =0.40×8+0.20×3+0,27×5=5.15
Теперь оценим загрузку ремонтных органов (рабочих), занятых ремонтом узлов 1 и 2. Узел 1 ремонтируется долю времени, равную
p1+p3=0.20+0.13=0.33. Узел 2 ремонтируется долю времени p2+p3=0.40.
Здесь уже может возникнуть вопрос об оптимизации решения. Допустим, что мы можем уменьшить среднее время ремонта того или другого узла (может быть, и того, и другого), но это нам обойдется в какуюто сумму. Спрашивается, выгодно ли это? Т. е. окупит ли увеличение дохода, связанное с ускорением ремонта, повышенные расходы на ремонт?
Задание
1. В моменты времени t1, t2, t3 производится осмотр ЭВМ. Возможны следующие состояния ЭВМ: полностью исправна, незначительные неисправности, существенные неисправности, ЭВМ полностью вышла из строя. Матрица переходных вероятностей имеет вид:
| 0,5 | 0,3 | 0,3 | ||
| P = | 0,4 | 0, 4 | 0, 2 | |
| 0,3 | 0,7 | |||
Построить граф состояний. Найти вероятности состояний ЭВМ после одного, двух и трех просмотров, если в начале (при t=0) ЭВМ была полностью исправна.
2. В городе издаются три журнала C1, С2, С3. Читатели выписывают один из них. Пусть в среднем читатели стремятся поменять журнал, т.е. подписаться на другой не более одного раза в год. Вероятности таких изменений постоянны. Результаты маркетинговых исследований спроса читателей даны следующем процентном соотношении:
80% читателей С1 подписываются на С2;
15% читателей С2 подписываются на С3;
8% читателей С3 подписываются на С1.
Требуется:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|