
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Запишите себе в тетрадь приведенные здесь примеры и сделайте необходимые рисунки.
№10 «Подземная разработка месторождений полезных ископаемых»
Дисциплина: Математика.
Преподаватель :Горяйнова Надежда Николаевна.
Группа № 10, 1 курс, «Подземная разработка месторождений полезных ископаемых».
Тема : Практическое занятие. Решение упражнений на вычисление физических величин с помощью определенного интеграла.
1.Лекция. На сегодняшнем занятии обобщим весь изученный материал об определенном интеграле и закрепим навыки его вычисления и применения.
Запишите себе в тетрадь приведенные здесь примеры и сделайте необходимые рисунки.
1. Вычисление определенных интегралов рассмотрим на примерах:
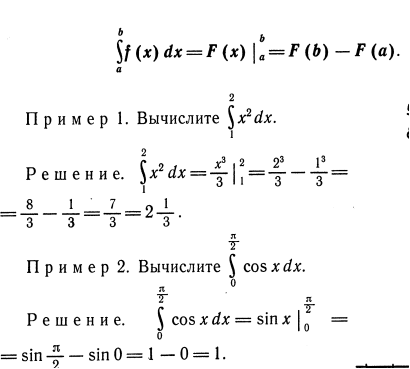
2. Применение определенного интеграла:
Задача 1.Найти площадь криволинейной трапеции изображенной на рисунке 154.
Решение:
По формуле: 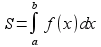 , находим
, находим 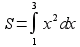 . Вычисли этот интеграл по формуле Ньютона-Лейбница
. Вычисли этот интеграл по формуле Ньютона-Лейбница 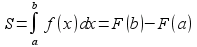 . Одной из первообразных функции
. Одной из первообразных функции 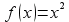 является
является 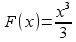 . Поэтому
. Поэтому 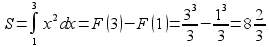 (кв.ед.)
(кв.ед.) 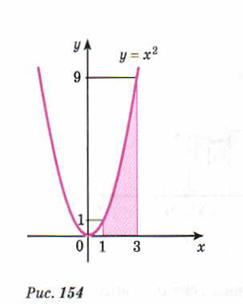
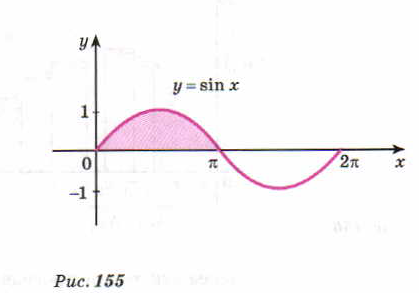
Задача 2.Найти площадь криволинейной трапеции изображенной на рисунке 155
Решение:
Функция 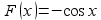 является первообразной для функции
является первообразной для функции 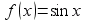 . По формулам
. По формулам 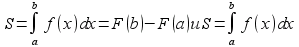 , получаем
, получаем 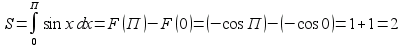 (кв.ед.)
(кв.ед.)
Задача 3.Найти площадь S фигуры, ограниченной параболой
у = х2 + 1 и прямой у = х + 3.
Решение:
Построим графики функций у = х2 + 1 и у = х + 3. Найдём абсциссы точек пересечения этих графиков из уравнения
х2 + 1 = х + 3. Это уравнение имеет корни х1=-1, х2= 2. Фигура, ограниченная графиками данных функций, изображена на рисунке 161. Из рисунка видно, что искомую площадь можно найти как разность площадей S, и S2 двух трапеций, опирающихся на отрезок [-1; 2], первая из которых ограничена сверху отрезком прямой у= х + 3, а вторая — дугой параболы у = х2+ 1. Так как 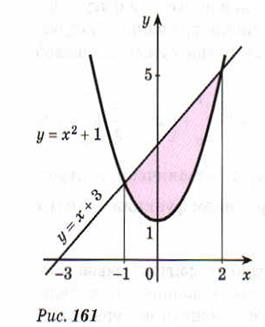
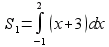 ,
,
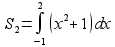 , то
, то 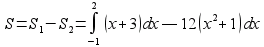 ,
,
Используя свойство первообразных, можно записать S в виде одного интеграла:
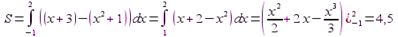
(кв. ед)

Контроль. Выполните самостоятельно следующие примеры:
1. Вычислить определенный интеграл:
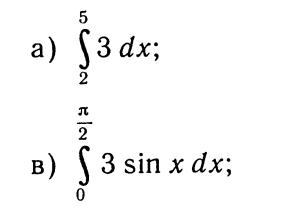
2. Вычислить площадь криволинейной трапеции, образованной линиями:
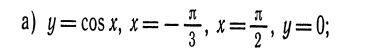
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|