Группа 1ОМД-2, Дисциплина «Математика»

Группа 1ОМД-2, Дисциплина «Математика»

08.06.2020

Подготовка к практической работе 29

Задание 1.Найти область решений системы неравенств:

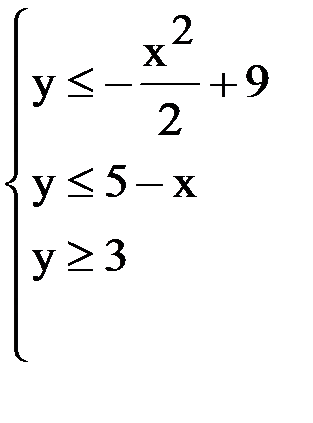
Решение.

1) Возьмем первое неравенство. Заменим знак неравенства на знак равенства, получим уравнение:

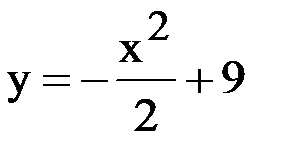– это квадратичная функция, график – парабола. Вершина в точке (0;9), ветви вниз. Возьмем несколько точек для её построения:

x		– 2		– 4
y

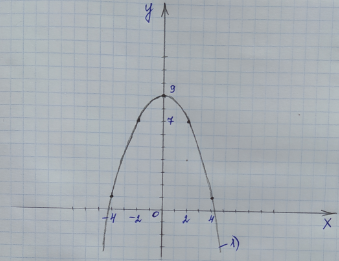
Теперь мы должны понять, где будет штриховка: внутри параболы или снаружи. Для этого берем любую точку на плоскости, только не на самой параболе. Возьмем точку с координатами (0;0). Подставляем координаты этой точки, а именно x=0 и y=0 в первое неравенство, которое дано в условии:

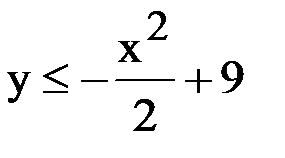
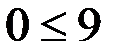– это неравенство верное, значит, наносим штриховку там, где находится выбранная нами точка (0;0), т. е. внутри параболы:

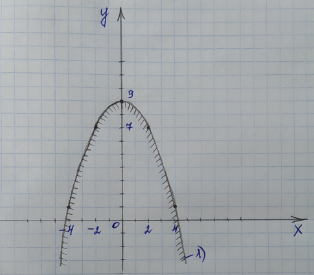
2) Возьмем второе неравенство. Заменим знак неравенства на знак равенства, получим уравнение:

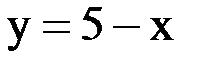– получили линейную функцию, графиком которой является прямая. Построим эту прямую, для этого возьмем любые две точки:

x
y

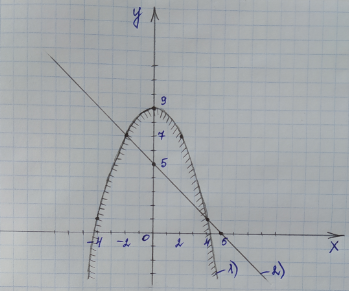
Теперь мы должны понять, в какую сторону направить штриховку: вверх от прямой или вниз от неё. Для этого берем любую точку выше прямой или ниже неё. Удобнее взять точку с координатами (0;0). Подставляем координаты этой точки, а именно x=0 и y=0 во второе неравенство, которое дано в условии:

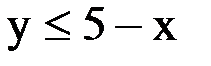
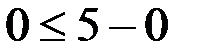
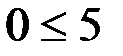– это неравенство верное, значит, направляем штриховку в ту сторону, где находится выбранная нами точка (0;0), т. е. вниз от данной прямой:

3) Возьмем третье неравенство. Заменим знак неравенства на знак равенства, получим уравнение: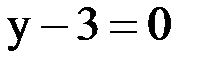

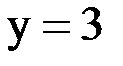– это прямая, параллельная оси Ох, проходящая через точку (0;3). Построим её на плоскости:

Теперь мы должны понять, в какую сторону направить штриховку: вверх от прямой или вниз от неё. Для этого берем любую точку выше прямой или ниже неё. Удобнее взять точку с координатами (0;0). Подставляем координаты этой точки, а именно x=0 и y=0 в третье неравенство, которое дано в условии:

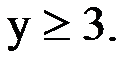
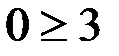– это неравенство неверное, значит, направляем штриховку в ту сторону, где не находится выбранная нами точка (0;0), т. е. вверх от данной прямой:

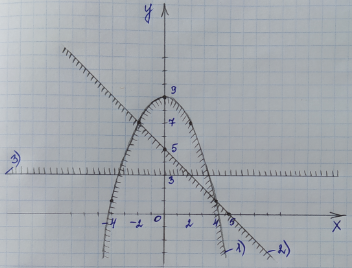
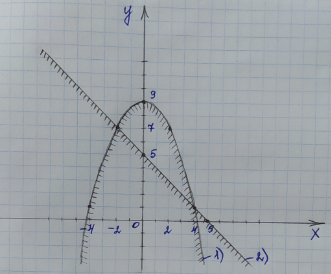
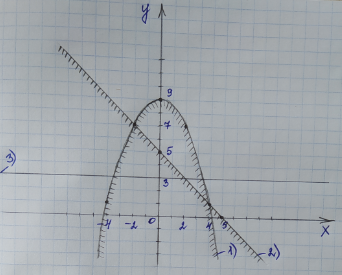
Теперь мы должны определить и закрасить (карандашом) область, которая ограничена со всех сторон данными тремя линиями. По рисунку видно, что это фигура ABC:

Ответ:Область решений – фигура ABC

Задача 2. Для полученного в задаче 1 множества точек аналитически найдите координаты точки, имеющей наибольшую ординату.

Решение.

У полученной фигуры АВС рассмотрим три точки А, В, С и выберем из них только одну точку, у которой наибольшая ордината, т. е. которая находится выше всех по оси Oy. По рисунку видно, что это точка В. Надо найти координаты этой точки, не используя график. Точка В находится на пересечении двух линий: параболы под номером 1) и прямой под номером 2). Значит, возьмем уравнения этих двух линий и составим из них систему уравнений:

Так как левые части этих уравнений равны, то приравняем их правые части:

Перенесем всё в левую часть:

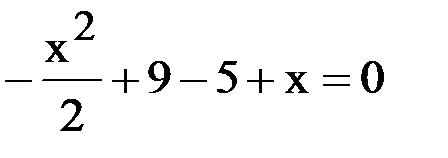
Приведем подобные слагаемые:

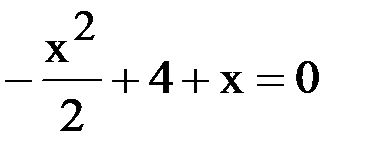
Умножим обе части уравнения на – 2:

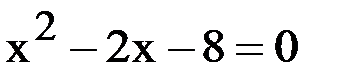
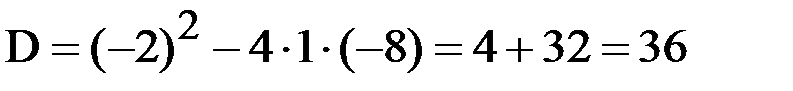
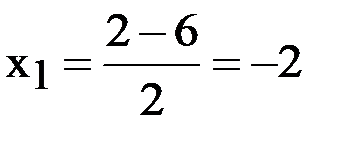
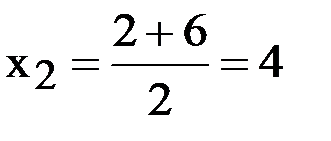
По графику видно, что не может являться абсциссой точки В, так как находится справа от оси Oy, а точка В лежит слева от оси Oy.

Значит, берем 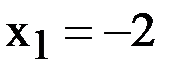. Теперь надо найти вторую координату y для точки В. Для этого подставим найденное значение 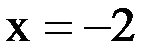в любое из уравнений системы. Выберем второе уравнение, так как оно проще:

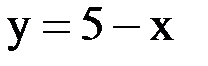
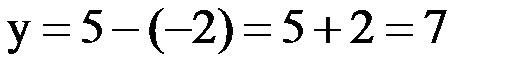
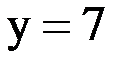
Ответ: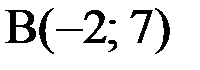

Задача 3. В летнем лагере на каждого участника полагается 20г сливочного масла в день. В лагере 156 человек. Сколько упаковок масла по 200г понадобится на 1 день?

Решение.

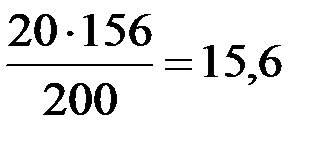
Купить 15,6 упаковок масла невозможно, поэтому берем 16 упаковок, чтобы хватило на всех.

Ответ:16 упаковок

Задача 4. Клиент хочет арендовать автомобиль на сутки для поездки протяжённостью 600 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму в рублях заплатить клиент за аренду и топливо, если выберет самый дешёвый вариант?

Автомобиль	Топливо	Расход топлива (л на 100 км)	Арендная плата (руб .за сутки)
	Дизельное
	Бензин
	Газ

Цена дизельного топлива 16 руб. за литр, бензина – 20,5 руб. за литр, газа – 15 руб. за литр

Решение.Рассчитаем стоимость поездки для каждого автомобиля:

А) 6·4·16+3400=3784

Б) 6·8·20,5+3000=3984

В) 6·11·15+3000=3990

Видно, что при выборе автомобиля 1 стоимость поездки будет наименьшей и составит 3784 рубля

Ответ:3784 рубля

Задача 5. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 148 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле 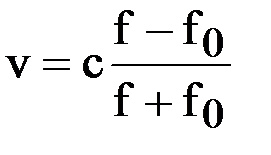, где с= 1500 м/с – скорость звука в воде, f₀ – частота испускаемых импульсов (в МГц), f – частота отражённого от дна сигнала, регистрируемого приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 20 м/с. Ответ выразите в МГц.

Решение.Составим неравенство:

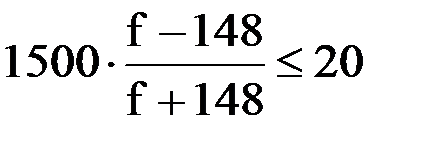
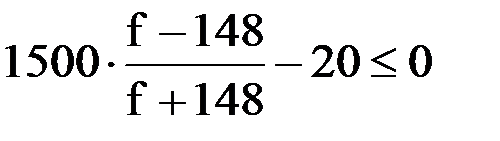
Приведем левую часть к общему знаменателю:

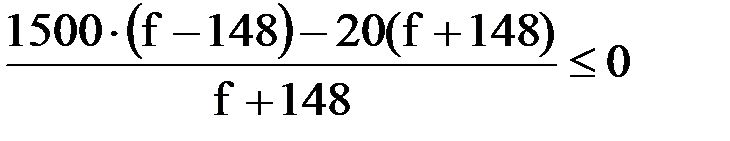
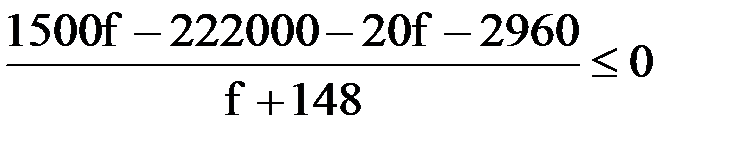
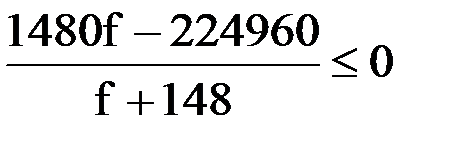
Решим данное дробно-рациональное неравенство методом интервалов:

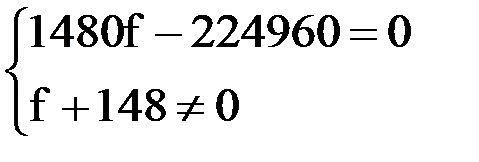
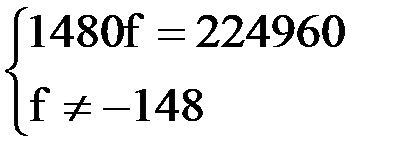
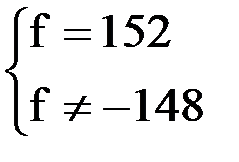
Нанесем найденные значения f на числовую прямую:

Теперь надо определить знак на каждом промежутке. Для этого возьмем любое значение f, например, 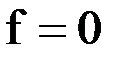из среднего промежутка и подставим в левую часть последнего неравенства: 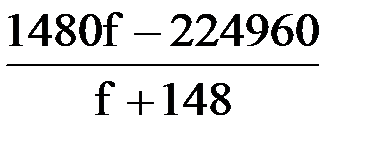, получим:

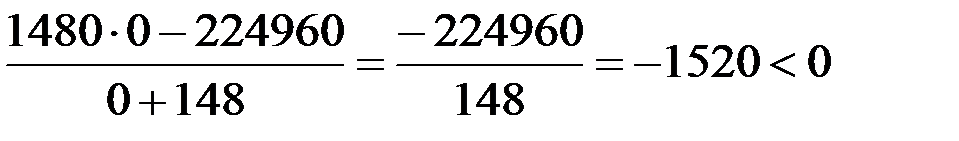, значит, на среднем промежутке знак «–». На остальных двух промежутках знаки будут чередоваться:

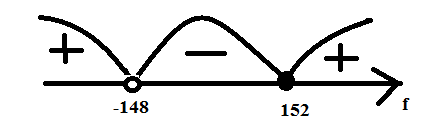
Так как мы решаем неравенство 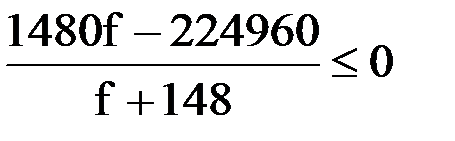, то решением его будут промежутки со знаком «–»: 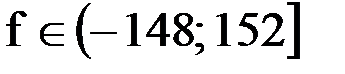. Из этих промежутков видно, что наибольшая частота f=152 МГц.

Ответ: .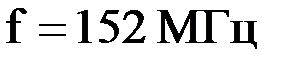

Домашнее задание.

Задача 1. Построить множество точек плоскости, координаты которых удовлетворяют соотношениям

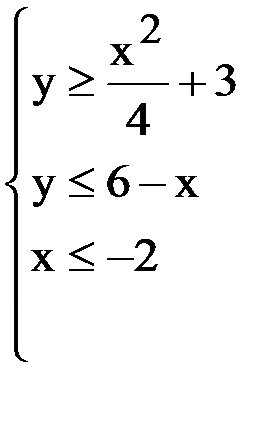
Задача 2.Для полученного в задаче №1 множества точек аналитически найдите координаты точки, имеющей наибольшую ординату.

Задача 3.На день рождения полагается дарить букет из нечётного числа цветов. Ромашки стоят 12 рублей за штуку. У Васи есть 170 рублей. Из какого наибольшего числа ромашек он может купить букет Маше на день рождения?