
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа 1ОМД-2, Дисциплина «Математика»
Группа 1ОМД-2, Дисциплина «Математика»
03.06.2020
Тема: Применение математических методов
для решения содержательных задач
1. Изображение на координатной плоскости множества решений
неравенств с двумя переменными
Пусть задано линейное неравенство с двумя переменными x и y:
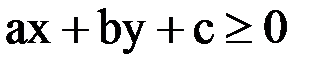 .
.
Совокупность точек плоскости, координаты которых удовлетворяют данному неравенству, называется областью решенийданного неравенства.
Областью решений неравенства является полуплоскость.
Задание 1. Найти полуплоскость, определяемую неравенством:
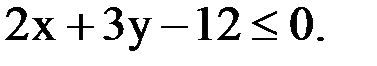
Решение.
Заменим знак неравенства на знак равенства, получим уравнение:
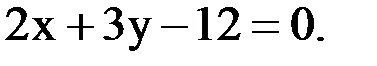
Выразим из этого уравнения y:
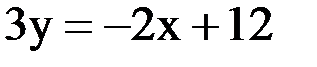

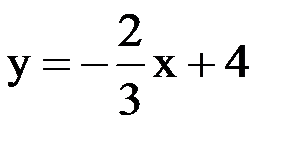
Получили линейную функцию, графиком которой является прямая. Построим эту прямую, для этого возьмем любые две точки:
| x | ||
| y |
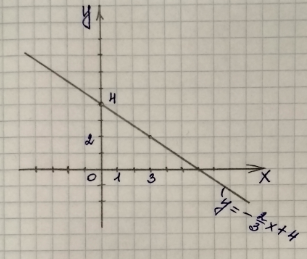
Данная прямая делит плоскость на две полуплоскости (выше прямой и ниже прямой). Мы должны определить, какая из двух полуплоскостей является решением данного неравенства.
Для этого берем любую точку на плоскости, например, точку с координатами (0;0). Подставляем координаты этой точки, а именно x=0 и y=0 в самое первое неравенство, которое дано в условии: 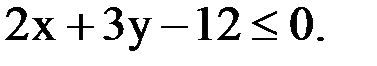
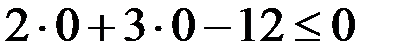
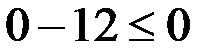
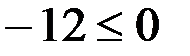 – это верное неравенство, значит, направляем штриховку в ту сторону, где находится выбранная нами точка (0;0), т. е. ниже данной прямой:
– это верное неравенство, значит, направляем штриховку в ту сторону, где находится выбранная нами точка (0;0), т. е. ниже данной прямой:

Задание 2. Найти полуплоскость, определяемую неравенством:
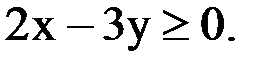
Решение.
Заменим знак неравенства на знак равенства, получим уравнение:
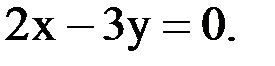
Выразим из этого уравнения y:
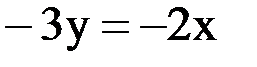
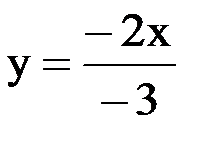
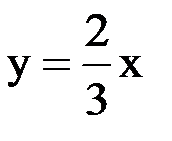
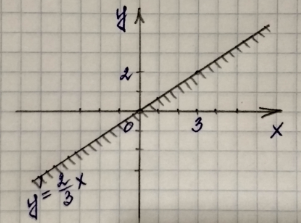
Получили прямую пропорциональность, графиком которой является прямая, проходящая через начало координат. Построим эту прямую, для этого возьмем любые две точки:
| x | ||
| y |
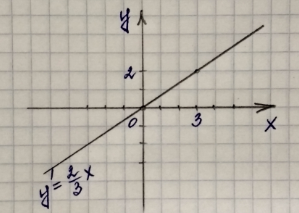
Данная прямая делит плоскость на две полуплоскости (выше прямой и ниже прямой). Мы должны определить, какая из двух полуплоскостей является решением данного неравенства.
Для этого берем любую точку на плоскости, например, точку с координатами (1;2). Подставляем координаты этой точки, а именно x=1 и y=2 в самое первое неравенство, которое дано в условии: 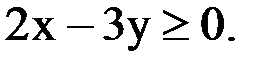
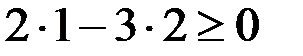
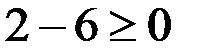
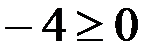 – это неравенство неверное, значит, направляем штриховку в ту сторону, где не находится выбранная нами точка (1;2), т. е. ниже данной прямой:
– это неравенство неверное, значит, направляем штриховку в ту сторону, где не находится выбранная нами точка (1;2), т. е. ниже данной прямой:
Домашнее задание.
Задание.Найти полуплоскость, определяемую неравенством:
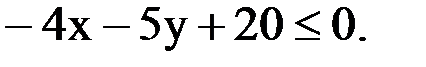
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|