МНОГОГРАННИКИ. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.

МНОГОГРАННИКИ. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.

Определение.Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.

Определение. Многогранник называется правильным, если все его грани - равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней. Все ребра правильного многогранника - равные отрезки, все плоские углы правильного многогранника также равны.

Определение.Многогранник называется выпуклым, если он весь лежит по одну сторону от плоскости любой его грани.

Определение.Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называется диагональю многогранника.

Определение. Выпуклый многогранник называется правильным, если:

1) все его грани – равные правильные многоугольники;

2) в каждой вершине сходится одинаковое количество граней;

3) все его двугранные углы равны.

Следствия. В правильном многограннике равны:

а) все ребра;

б) все плоские и многогранные углы и в каждой вершине сходится одинаковое количество ребер.

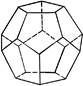
Существует всего пять правильных многогранников:

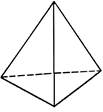
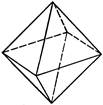
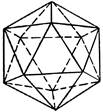
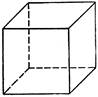
Правильный тетраэдр	Правильный октаэдр	Правильный икосаэдр	Куб (гексаэдр)	Правильный додекаэдр

Составлен из четырёх равносторонних треугольников	Составлен из восьми равносторонних треугольников.	Составлен из двадцати равносторонних треугольников	Составлен из шести квадратов	Составлен из двенадцати правильных пятиугольников

Следствие. Выпуклых многогранников, у которых в каждой грани больше пяти ребер или в каждой вершине сходится более пяти ребер не существует.

Теорема Эйлера:Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2

Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В - Р = 2

Правильный многогранник	Число
Правильный многогранник	граней	вершин	рёбер
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр