Определенный интеграл и его свойства

Дисциплина: Математика.

Преподаватель :Горяйнова Надежда Николаевна.

Группа № 4, 2 курс, «Мастер отделочных строительных работ»

Тема урока: Повторение. Первообразная и интеграл

1.Лекция. На сегодняшнем занятии повторим первообразную, определенный интеграл и его применение. Воспользуемся учебником «Алгебра и начала математического анализа», 10-11 кл. , Ч.1., Мардкович А.Г.

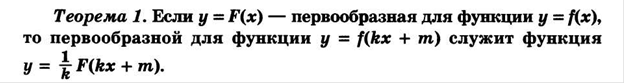
Весь этот материал вы можете посмотреть в своем конспекте.

Определенный интеграл и его свойства

Пусть функция 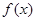определена на отрезке 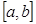. Разобьем отрезок на n частей точками 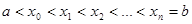, выберем на каждом элементарном отрезке 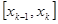произвольную точку x_k и обозначим через 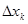длину каждого такого отрезка.

Интегральной суммой для функции 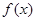на отрезке 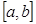называется сумма вида

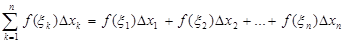
Определение: Определенным интегралом от функции 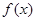на отрезке 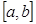называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

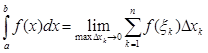
Для любой функции 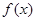, непрерывной на отрезке 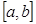, всегда существует определенный интеграл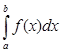

Простейшие свойства определенного интеграла

1)Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:

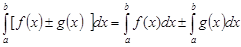
2) Постоянный множитель можно выносить за знак определенного интеграла

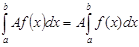
3) При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

4) Определенный интеграл с одинаковыми пределами равен нулю: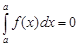

5) Отрезок интегрирования можно разделить на части:

с- точка, лежащая между а и b.

6) Если 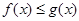на отрезке 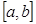, то .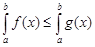

Для вычисления определенного интеграла от функции 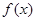, в том случае , когда можно найти соответствующую первообразную 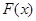, служит формула Ньютона-Лейбница:

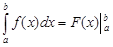=F(b)-F(a)

Рассмотрим нахождение простейших определенных интегралов. Запишите себе в конспект все примеры, вспомните , как это делается.

12 Следующая ⇒