Объём пирамиды. Задание #1. Задание #2. Задание #3. Задание #4. Задание #5. Задание #6

Объём пирамиды

Задание #1

Вопрос:

Высота треугольной пирамиды равна 2 см, а площадь основания равна 24 см2. Вычислите объем пирамиды. В ответ запишите только число без единиц измерения, например, 5

Запишите число: ___________________________

Задание #2

Вопрос:

Как изменится объём правильной пирамиды, если сторона основания не изменится, а высота уменьшится в 4 раза.

Выберите один из 4 вариантов ответа:

1) увеличится в 2 раза

2) увеличится в 4 раза

3) уменьшится в 2 раза

4) уменьшится в 4 раза

Задание #3

Вопрос:

Большим диагональным сечением правильной шестиугольной пирамиды является равносторонний треугольник, сторона которого равна 10м. Вычисли объём пирамиды. В ответ запиши только число без единиц измерения. Если получится дробное число, то записать его десятичной дробью, отделяя целую часть от дробной запятой. Например, 4,6

Запишите число: ___________________________

Задание #4

Вопрос:

Вычисли объём правильной усечённой треугольной пирамиды, если стороны её оснований равны 8 см и 12 см, а перпендикуляр, который соединяет основания, равен 93√3 см. В ответ запишите только число, без указания единиц измерения. Например, 6

Запишите число: ___________________________

Задание #5

Вопрос:

Выберите верное утверждение

Выберите один из 4 вариантов ответа:

1) Объем пирамиды равен одной трети произведения площади основания на высоту.

2) Объем пирамиды равен произведению площади основания на высоту.

3) Объем пирамиды равен одной трети произведения периметра основания на высоту.

4) Объем пирамиды равен произведению периметра основания на высоту.

Задание #6

Вопрос:

Выберите верное утверждение:

Выберите один из 4 вариантов ответа:

1) Объём усеченной пирамиды, высота которой равна h, а площадь оснований равны S и S₁, вычисляется по формуле:

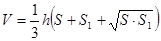
2) Объём усеченной пирамиды, высота которой равна h, а площадь оснований равны S и S₁, вычисляется по формуле:

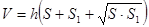
3) Объём усеченной пирамиды, высота которой равна h, а площадь оснований равны S и S₁, вычисляется по формуле:

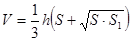
4) Объём усеченной пирамиды, высота которой равна h, а площадь оснований равны S и S₁, вычисляется по формуле:

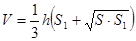
Задание #7

Вопрос:

В правильной шестиугольной пирамиде сторона основания равна 2 см, объем пирамиды равен 6 см³. Чему равна высота пирамиды?

Выберите один из 3 вариантов ответа:

1) 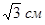2) 3 см 3)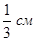

Задание #8

Вопрос:

Объем пирамиды равен 56 см³, а площадь основания равна 14 см². Чему равна высота пирамиды?

Выберите один из 3 вариантов ответа:

1) 14 см 2) 12 см 3) 16 см

Задание #9

Вопрос:

В правильной треугольной пирамиде высота равна 5 см, стороны основания равны 3 см. Чему равен объем пирамиды?

Выберите один из 3 вариантов ответа:

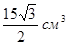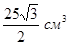1) 2) 3)

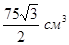
Задание #10

Вопрос:

Объем правильной четырехугольной пирамиды равен 27 см³, высота равна 9 см. Найдите сторону основания.

Выберите один из 3 вариантов ответа:

1) 12 см

2) 9 см

3) 3 см