
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРОГРАММА. Колебания
ПРОГРАММА
курса «Теория колебаний и волн», группа 6306(61062014pmf@gmail.com)
Колебания
Введение.Колебательные процессы.Основные понятия и способы описания. Примеры колебательных систем. Общность моделей и методов анализа колебательных систем.
‚ Малые колебания с постоянной частотой.Свободные колебания малой амплитуды. Модель гармонического осциллятора. Точное решение при произвольных начальных условиях. Амплитуда, частота, период, начальная фаза колебаний, декремент, логарифмический декремент, добротность, энергия колебаний.
ƒВынужденные колебания малой амплитуды. Метод комплексификации. Резонанс. Статическое смещение. Ширина резонансной кривой. Произвольная внешняя сила. Спектр колебаний.
„ Колебания малой амплитуды с меняющейся под действием внешних факторов частотой. Медленное изменение параметров. Адиабатические инварианты. Быстрое изменение параметров.
…Сравнимые частоты. Параметрический резонанс. Метод ван дер Поля. Укороченные уравнения.
† Связанные колебания.Свободные колебания двух связанных математических маятников. Емкостная и индуктивная связь. Нормальные и парциальные частоты. Синфазные и противофазные колебания. Вынужденные колебания двух связанных математических маятников. Фильтры.
‡ Нелинейные колебания. Свободные колебания математического маятника произвольной амплитуды. Интегрирование консервативных систем 2-го порядка. Качественные методы анализа нелинейных колебаний. Метод фазовой плоскости Особые точки: центр, фокус, узел, седло. Аттракторы. Фазовый портрет.
ˆМетоды приближенного анализа колебательных систем.
‰Генератор ван дер Поля. Автоколебания. Предельный цикл.
Волны
Œ Колебания малой амплитуды в цепочке связанных гармонических осцилляторов. Предельный переход к волновому процессу. Волновое уравнение.Волны малой амплитуды.Бегущие и стоячие волны. Амплитуда, частота, период, начальная фаза. Фронт волны. Плоские, цилиндрические и сферические волны.
Примеры волновых процессов. Электромагнитные волны. Акустические волны. Диспергирующие среды. Волны на воде. Группы волн. Фазовая и групповая скорости. Энергия и импульс волн.
Ž Ограниченные среды. Одномерные стоячие волны. Свободные и вынужденные колебания струны. Метод Фурье. Волноводы и объемные резонаторы. Классификация волн в ограниченных средах.
Акустические волны в волноводах и резонаторах.
Электромагнитные волны в резонаторах с металлическими стенками. Диэлектрические волноводы.
‘ Простые волны. Уравнение Римана. Слабые ударные волны. Уравнение Бюргерса.
’ Волны популяций и эпидемий. Уравнение Колмогорова-Петровского-Пискунова.
U Сдача семестрового задания.
Литература
1. Н. В. Карлов, Н. А. Кириченко. Колебания, волны, структуры М.: Физматлит, 2003. - 496 с.
2. И. П. Завершинский, Е. Я. Коган. Теория колебаний и волн Самара: Изд-во СГАУ, 2007. - 159 с.
3. М. И. Рабинович, Д. И. Трубецков. Введение в теорию колебаний и волн. М.: Наука, 1984. 432 с.
4. А. П. Кузнецов, Д. И. Трубецков, А. Г. Рожнёв. Линейные колебания и волны: Сб. задач. М.: Физматлит, 2001. 128 с.
Примечание:
1. Лабораторные работы делаются и сдаются непрерывно в соответствии с графиком выполнения и сдачи работ. Для получения зачета необходимо сдать8работ.
2. Семестровое задание состоит из задач разной сложности. Сдача семестрового задания – допуск к зачету.
3. Самостоятельные работы проводятся 3 раза в семестр, состоят из 10 тестовых вопросов, касающихся теоретических положений курса. К каждому тестовому вопросу как правило предлагается 4 ответа.
Семестровое задание
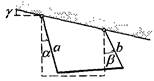 1. Космический корабль вращается вокруг своей оси с угловой скоростью W. Как зависит период колебаний маятника длины l от расстояния R точки подвеса до оси вращения? Плоскость колебаний проходит через ось вращения.
1. Космический корабль вращается вокруг своей оси с угловой скоростью W. Как зависит период колебаний маятника длины l от расстояния R точки подвеса до оси вращения? Плоскость колебаний проходит через ось вращения.
2. Палочка длины 2l подвешена на двух вертикальных нитях длины а и b. Определить частоту плоских малых колебаний.
3. Стакан массой m1 = 20 г и площадью поперечного сечения S = 5 см2 содержит ртуть массой m2 = 80 r и плавает на поверхности воды. Под действием вертикальной силы стакан выводится из положения равновесия и отпускается. Определить период колебаний системы.
4. На частоте f емкостное сопротивление колебательного контура равно 250 Ом, индуктивное – 160 Ом, резистивное 4 Ом. Определить добротность контура.
5. При какой скорости поезда рессоры вагонов будут колебаться с наибольшей амплитудой под действием толчков колес о стыки рельсов, если длина рельсов 12,5 м, нагрузка на рессору 5,5 т., а рессора прогибается на 16 мм при нагрузке на нее в 1 т?
6. Из одинаковых элементов L = 64 мкГ, C = 400 пФ, R = 20 Ом собраны параллельный и последовательный колебательный контуры. Во сколько раз отличаются их сопротивления на резонансной частоте?
7. На последовательный колебательный контур действуют одновременно сигнал с резонансной частотой U(t) = 1×cos106t мВ и помеха V(t) = 10×cos5×105t мВ. Рассчитать параметры L, C и R, если известно, что на емкости С напряжение сигнала в 10 раз превышает напряжение помехи, а амплитуда составляющей тока с частотой сигнала равна 100 мА.
8. Мальчик раскачивает качели, дважды за период колебаний резко приседая и резко выпрямляя ноги. В какие именно моменты он должен делать это, чтобы качели раскачивались наиболее быстро? Найти приращение энергии колебаний за период.
9. Частица массой m движется по круговой орбите радиусом R в поле центральных сил, потенциал которого равен -km/rn. Показать, что если n < 2, то круговая орбита устойчива по отношению к малым колебаниям (т. е. частица осциллирует около круговой орбиты).
10. Найти особые точки и построить фазовый портрет модифицированной системы хищник-жертва, учтя конкуренцию между жертвами за ресурс.
 11. Поршень массы m находится в цилиндре, установленном вертикально. В состоянии равновесия расстояние от дна цилиндра до поршня h = 20 см. В цилиндре под поршнем азот. Записать уравнение колебаний поршня. Найти условие малости колебаний и частоту малых колебаний. Построить фазовый портрет.
11. Поршень массы m находится в цилиндре, установленном вертикально. В состоянии равновесия расстояние от дна цилиндра до поршня h = 20 см. В цилиндре под поршнем азот. Записать уравнение колебаний поршня. Найти условие малости колебаний и частоту малых колебаний. Построить фазовый портрет.
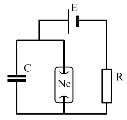
12. Покажите, что релаксационный генератор на неоновой лампе, изображенный на рисунке, описывается уравнением 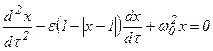 . Найти особые точки, построить фазовый портрет системы и получить укороченные уравнения методом ван дер Поля.
. Найти особые точки, построить фазовый портрет системы и получить укороченные уравнения методом ван дер Поля.
 13. Найти резонансную частоту системы из двух индуктивно связанных контуров. Первичный контур настроен на частоту f01 = 100 кГц и является колебательным, вторичный контур – апериодический (wL2 >> R2), коэффициент связи k = 60 %.
13. Найти резонансную частоту системы из двух индуктивно связанных контуров. Первичный контур настроен на частоту f01 = 100 кГц и является колебательным, вторичный контур – апериодический (wL2 >> R2), коэффициент связи k = 60 %.
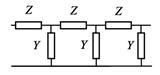
14. Обобщенная радиотехническая цепочка, по которой могут распространяться волны, имеет вид, показанный на рисунке. Здесь Z - обобщенный комплексный импеданс, а Y - обобщенная комплексная проводимость. Найдите для нее закон дисперсии.
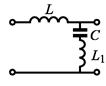 15. Имеется радиотехническая цепочка, составленная из емкостей и индуктивностей. Одно звено каждой цепочки показано на рисунке) Перейдите к волновому приближению (длина волны гораздо больше периода цепочки). Найдите и нарисуйте закон дисперсии. 2) Постройте графики зависимости фазовой и групповой скорости от волнового числа.
15. Имеется радиотехническая цепочка, составленная из емкостей и индуктивностей. Одно звено каждой цепочки показано на рисунке) Перейдите к волновому приближению (длина волны гораздо больше периода цепочки). Найдите и нарисуйте закон дисперсии. 2) Постройте графики зависимости фазовой и групповой скорости от волнового числа.
16. Оцените силу натяжения гитарной струны, издающей звук до четвертой октавы.
17. Дисперсионное уравнение электромагнитной волны в вакууме имеет вид w2 =с2k2, где с - скорость света. Как будет выглядеть дисперсионное в системе отсчета, двигающейся со скоростью v по отношению к исходной?
18. Как зависит скорость звука в квадратном волноводе со стороной l от его площади? Здесь l << l, l - длина волны звука.
19. Определите первую резонансную частоту колебаний воздуха между двумя параллельными зданиями, находящимися на расстоянии 20 м друг от друга. Высота зданий заметно больше этого расстояния. Скорость звука в воздухе с = 330 м/с.
20. Определить частоту колебаний основного тона столба воздуха в органной трубе, открытой с одного конца. Длина трубы l = 85 см, температура воздуха 20 °C.
21. Прямоугольный коридор имеет ширину 2 м, высоту 3 м и длину 10 м. Найти число возбужденных мод DN помещения в интервале частот от f до f + df в зависимости от частоты f для значений f, равных 100 Гц и 1000 Гц, df = 5 Гц.
 22. В кубическом резонаторе с вакуумным наполнением и идеально проводящими стенками (сторона квадрата равна L) возбуждена основная мода. Электрическое поле
22. В кубическом резонаторе с вакуумным наполнением и идеально проводящими стенками (сторона квадрата равна L) возбуждена основная мода. Электрическое поле 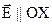 , амплитуда поля Е0. Определить вектор Пойнтинга, как функцию координат и времени.
, амплитуда поля Е0. Определить вектор Пойнтинга, как функцию координат и времени.
23. Однородный канат длиной l подвешен вертикально за один конец и растянут под действием собственной силы тяжести. На нижнем конце каната возбуждается колебание, которое распространяется вверх в виде волны. Определить скорость распространения волны и время прохождения волной всей длины каната
24. Определить погонные параметры коаксиального кабеля без потерь с характеристическим сопротивлением R = 75 Ом, если известно, что электромагнитные волны распространяются в нем со скоростью 1011 мм/с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|