
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Классная работа. Интегралы. Изучение нового материала. Таблица неопределенных интегралов. Свойства неопределенного интеграла. Примеры. Выполняем задания из учебника №20.42-20.46(а,г) 20.47а.
18.05.20. Классная работа. Интегралы
1.Повторим тему Первообразная.
Выполните задания
1. Докажите, что F(х) = х3 – 2sinx является первообразной для f(х) = 3х2 – 2cosx.
2. Для функции у = f(х) найдите общий вид первообразных:
а) f(х) = 2sinx + 3cos5x
б) f(х) = 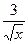 + х2
+ х2
в) f(х) = 
г) f(х) = 
д) f(х) = 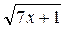
е) f(х) = sin3x – 
ж) f(х) = 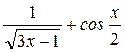
з) f(х) = 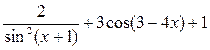 .
.
3. Для функции f(х) = 4х – 6х2 + 1 найти первообразную, график которой проходит через точку М (1;3).
4. Для функции f(х) = sinx – cosx найти первообразную, принимающую заданное значение в данной точке F( 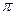 ) = 2
) = 2
2. Изучение нового материала
Существует 2 вида интегралов: неопределённый и определённый.
Сегодня мы знакомимся с неопределённым интегралом
Определение: Если функция 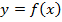 имеет на промежутке
имеет на промежутке 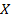 первообразную
первообразную 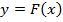 , то множество всех первообразных, т. е. множество функций
, то множество всех первообразных, т. е. множество функций 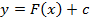 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 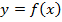 и обозначается
и обозначается
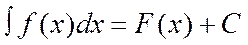 читают: «неопределённый интеграл эф от икс по дэ икс
читают: «неопределённый интеграл эф от икс по дэ икс
f(x) – подынтегральная функция; 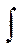 и dxзнак интеграла; F(x) первообразная функции
и dxзнак интеграла; F(x) первообразная функции
+С –общий вид указывается
Можно получить таблицу неопределенных интегралов. Она получается из таблицы первообразных
Таблица неопределенных интегралов
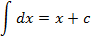
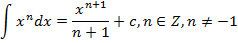
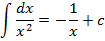
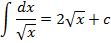
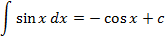
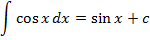

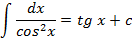 и т.д.!!!
и т.д.!!!
Свойства неопределенного интеграла
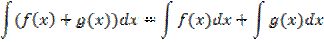
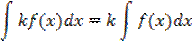
Если  , то
, то 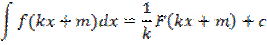
Примеры
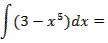
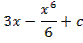
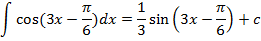
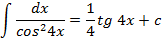
Выполняем задания из учебника №20.42-20.46(а,г) 20.47а.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|