Хелпикс

Главная

Контакты

Случайная статья



Методы решения иррациональных уравнений.

Стр 1 из 3Следующая ⇒


 

 

 

Методы решения иррациональных уравнений.


 

I) Метод возведения в четные степени (неравносильный переход нужна проверка) и нечетные степени (равносильный переход).

 

II) Уравнения вида  решаются следующим образом.

Уравнению вида 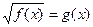 соответствует равносильная система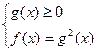

 

III) Уравнения вида  решаются следующим образом.

Так как произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а остальные при этом имеют смысл, то данное уравнение равносильно следующей совокупности.

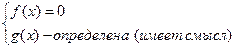                   или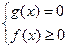

 

IV) Уравнения вида  решаются следующим образом.

Уравнению вида 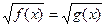 соответствует равносильная система.

Способ №1 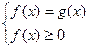           Способ №2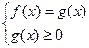

 

V) Уравнения вида  решаются следующим образом.

Уравнению вида 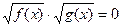 соответствует равносильная система.

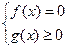         или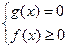           

 

VI) Уравнения вида  решаются следующим образом.

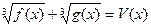
Возведем обе части уравнения в куб.

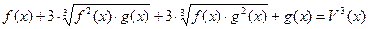
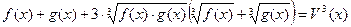(1)


                                             

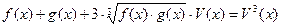                   (2)

При пепеходе из 1 в 2 происходит не равносильный переход, значит, необходима обязательная проверка.

 

VII) Уравнения вида  решаются следующим образом.

Уравнению вида 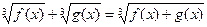 соответствует равносильная совокупность систем.


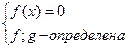
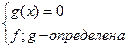
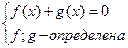
VIII) Уравнения вида  решаются следующим образом.

Уравнению вида 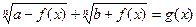решаются с помощью введения переменных.

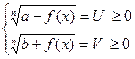
Сводятся к решению системы алгебраических уравнений.

 


123Следующая ⇒
  

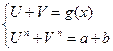
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.