
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Преподаватель - Брыкало А.А.. Конспект урока «Математика». Ход урока
Преподаватель - Брыкало А.А.
brukalo_aa@mail.ru
https://vk.com/id399759339
Конспект урока «Математика»
Дата18.05.2020
Группа87профессия«Машинист крана (крановщик)» курс2
Тема 108: «Числовые функции. Свойства числовых функций»
Форма работы:индивидуальная, электронное обучение
Тип урока:урок обобщения и повторения материала
Продолжительность урока: 1 час
Цель урока: повторить материал по теме « Числовые функции. Свойства функций»
Используемая литература:
Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г
Интернет-ресурсы:
Методика преподавания математики http://methmath.chat.ru/
Ход урока
Организационный этап:
Мотивационный модуль
С сегодняшнего занятия мы будем повторять весь материал за весь курс обучения. Тема сегодняшнего урока «Числовые функции. Свойства числовых функций».
Основная часть:
Объясняющий модуль
Теоретический материал для повторения
1. Определение числовой функции
Числовой функцией с областью определения D называется соответствие, при которой каждому числу x из множества D ставится в соответствие единственное число у, которая обозначается y=f(x), х-аргумент (независимая переменная), у-функция (зависимая переменная).
2. Свойства числовых функций
| Свойства функции | Определение | Геометрическая интерпретация |
| Область определения Обозначение: D, D(y). | Множество тех действительных значений аргумента 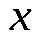 , при которых выражение , при которых выражение 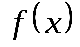 не теряет смысла и приобретает действительные значения не теряет смысла и приобретает действительные значения
| Проекция графика функции на ось абсцисс( 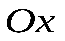 ) )
|
| Множество значений Обозначение: Е, Е(у). | Множество всех значений, которые приобретает функция, при всех значениях аргумента с области определения функции | Проекция графика функции на ось ординат( 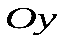 ) )
|
| Нули функции | Значение аргумента, при котором функция равна нулю, т.е. корни уравнения 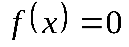
| абсциссы точек пересечения графика функции с осью 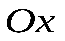 . .
|
| Промежутки знакопостоянства | Промежутки, на которых функция положительна или отрицательна, т.е. решения неравенства 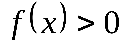 и и 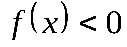
| Отрезки оси 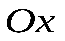 , которые соответствуют точкам графика функции, расположенных выше(ниже) оси , которые соответствуют точкам графика функции, расположенных выше(ниже) оси 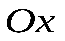
|
| Промежутки монотонности (промежутки, на которых функция возрастает или убывает) | Функция 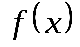 называется возрастающей на множестве называется возрастающей на множестве  , если для любых точек , если для любых точек  и и 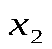 этого множества – таких, что этого множества – таких, что 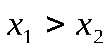 , - , - 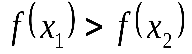 ;
убывающей, если ;
убывающей, если 
| Отрезки оси 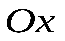 , где график «идет вверх» (вниз) , где график «идет вверх» (вниз)
|
| Наибольшее и наименьшее значения функции | Ординаты «самой высокой» и «самой низкой» точек графика | |
| Четность и нечетность функции | Если область определения функции
 симметрична относительно нуля и симметрична относительно нуля и  , то функция четная,
если , то функция четная,
если 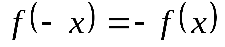 , то функция нечетная. , то функция нечетная. 
| График симметричен относительно оси ординат График симметричен относительно начала координат |
3.Основные виды элементарных функций и их графики
Линейная функция 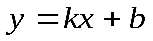
| Обратная пропорциональность 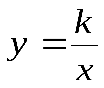 
| Квадратичная
функция 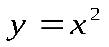
|
 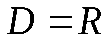 , , 
| 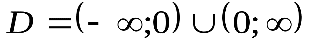
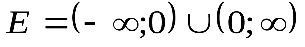
|  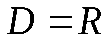 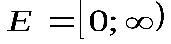
|
Квадратный
корень 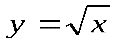
| Кубическая функция 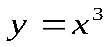
| 
|
 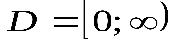 , , 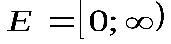
|  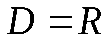 , , 
|  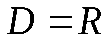 , , 
|
Запомни: Функции обладают следующими свойствами:
1.Область определения
2.Область значений
3.Нули функции
4.Монотонность функции
5.Промежутки знакопостоянства
6.Четность или нечетность
7.Наибольшее или наименьшее значение функции
8.Выпуклость функции
9.Ограниченность функции
10.Непрерывность функции
Тренировочный модуль
Задание №1
Найти экстремумы функции у= x3 – 3х + 1
Решение:
1.Найдем критические точки функции, для этого вычислим производную заданной функции
y'=3x2-3
2.Приравняем её к нулю и найдем корни полученного квадратного уравнения
3x2-3=0
x2-1=0
x1=-1 и x2=1
Получили 2 критические точки x1=-1 и x2=1
3. Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах.

В точке x1=-1 производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума
ymax = у(-1) = (-1)3 – 3(-1) +1 = -1+3 +1 =3
В точке x2=1 производная меняет знак с «-» на «+», значит в этой точке минимум. Значение минимума соответственно равно
ymin = у(1) =13-3*1+1 = -1
Ответ ymax= 3; ymin= -1
Задание №2
Найти точки экстремума функции f(x)=x3+6x2-15+7 и значения функции в этих точках.

Домашнее задание:
Составьте опорный конспект
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|