Преподаватель - Брыкало А.А.. Конспект урока «Математика». Ход урока

Преподаватель - Брыкало А.А.

brukalo_aa@mail.ru

https://vk.com/id399759339

Конспект урока «Математика»

Дата05.06.2020

Группа87профессия«Машинист крана (крановщик)» курс2

Тема 130-131:Практическое занятие №70 «Решение логарифмических уравнений и неравенств»

Форма работы:индивидуальная, электронное обучение

Тип урока:урок совершенствования знаний, умений и навыков

Продолжительность урока: 2 часа

Цель урока:систематизировать знания о решении логарифмических уравнений и неравенств, углубить знания при решении уравнений и неравенств.

Используемая литература:

Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

Интернет-ресурсы:

Методика преподавания математики http://methmath.chat.ru/

Ход урока

Организационный этап:

Мотивационный модуль

Ребята, на этом уроке вы повторите материал по теме «Решение логарифмических уравнений и неравенств», выполните практическую работу.

Основная часть:

Объясняющий модуль

Теоретический материал для самостоятельного изучения

1. Повторите теоретический материал.

1. Определение логарифмической функции.

Функцию вида 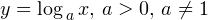называют логарифмической функцией.

Основные свойства логарифмической функции y = loga x:

	a > 1	0 < a < 1
Область определения	D(f) = (0; +∞)	D(f) = (0; +∞)
Область значений	E(f) = (-∞; +∞)	E(f) = (-∞; +∞)
Монотонность	Возрастает на (0; +∞)	Убывает на (0; +∞)
Непрерывность	Непрерывная	Непрерывная
Выпуклость	Выпукла вверх	Выпукла вниз

Графиком логарифмической функции является логарифмическая кривая:

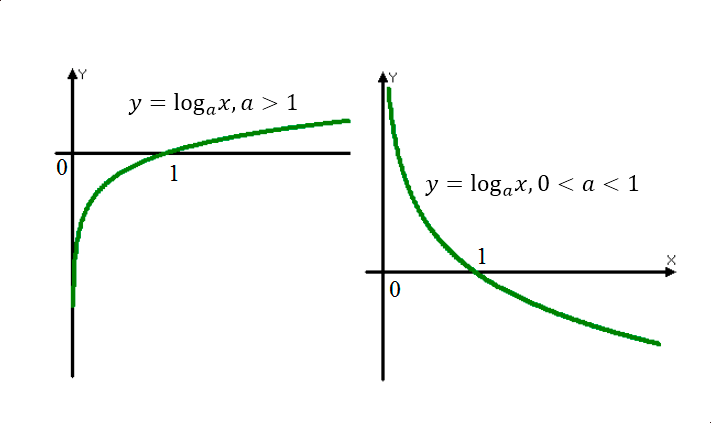
Свойства логарифмов

• Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

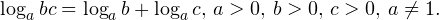
• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:

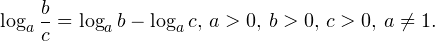
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:

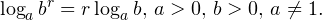
• Равенство log a t = log a s, где a > 0, a ≠ 1, t > 0, s > 0, справедливо тогда и только тогда, когда t = s.

• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):

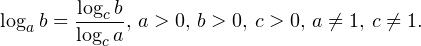
Теорема 1. Если f(x) > 0 и g(x) > 0, то логарифмическое уравнение log a f(x) = log a g(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).

2. Решение логарифмических уравнений

Пример 1. Решите уравнение:

Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:

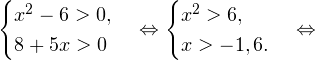
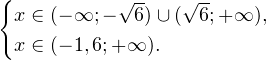
С учетом того, что

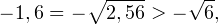
получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения:

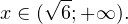
На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению:

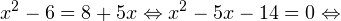
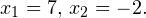
В область допустимых значений входит только первый корень.

Ответ: x = 7.

3. Решение логарифмических неравенств

Пример 2. Решите неравенство:

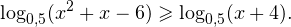
Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:

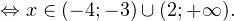
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству:

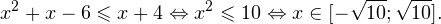
Окончательно, с учетом области допустимых значений получаем ответ:

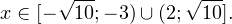
Выполнение практической части работы

2.Оформление работы:

Практическое занятие № 70

Тема: «Решение логарифмических уравнений и неравенств»

Цель: корректировать знания, умения и навыки по теме «Решение логарифмических уравнений и неравенств», закрепить и систематизировать знания по данной теме.

Практическая часть работы:

1. Решите уравнение:

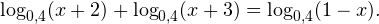
2. Решите уравнение:

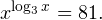
3.Решите уравнение:

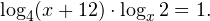
4. Решите неравенство:

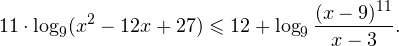
5. Решите логарифмическое неравенство:

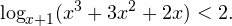
Домашнее задание:

Оформить отчет по практической работе