Преподаватель - Брыкало А.А.. Конспект урока «Математика». Ход урока

Преподаватель - Брыкало А.А.

brukalo_aa@mail.ru

https://vk.com/id399759339

Конспект урока «Математика»

Дата12.05.2020

Группа84профессия«Автомеханик» курс2

Тема 135:«Перпендикулярность прямых и плоскостей»

Форма работы:индивидуальная, электронное обучение

Тип урока:урок обобщения и повторения материала

Продолжительность урока: 1 час

Цель урока:повторить материал по теме «Перпендикулярность прямых и плоскостей»

Используемая литература:

Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

Интернет-ресурсы:

Методика преподавания математики http://methmath.chat.ru/

Ход урока

Организационный этап:

Мотивационный модуль

Тема сегодняшнего урока «Перпендикулярность прямых и плоскостей».

Основная часть:

Объясняющий модуль

Теоретический материал для самостоятельного изучения

1. Повторите теоретический материал.

1. Перпендикулярность прямой и плоскости

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90⁰

Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

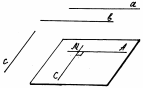
Рис.1

Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в плоскости.

Говорят также, что плоскость перпендикулярна к прямой а.

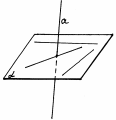
Рис.2

Если прямая а перпендикулярна к плоскости , то она, очевидно, пересекает эту плоскость. В самом деле, если бы прямая а не пересекала плоскость , то она лежала бы в этой плоскости или была бы параллельна ей.

Но в том и в другом случае в плоскости имелись бы прямые, не перпендикулярные к прямой а, например прямые, параллельные ей, что невозможно. Значит, прямая а пересекает плоскость .

Связь между параллельностью прямых и их перпендикулярностью к плоскости:

- если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

- если две прямые перпендикулярны к плоскости, то они параллельны.

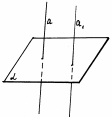
Рис.3

Признак перпендикулярности прямой и плоскости

Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

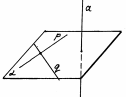
Рис.4

Замечания.

1.Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой, и притом единственная.

2.Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

3. Если две плоскости перпендикулярны к прямой, то они параллельны.

2. Примеры решения задач

Задача 1. Прямая РQ параллельна плоскости α (рис. 5). Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках Р₁ и Q₁. Докажите, что PQ = P₁Q₁.

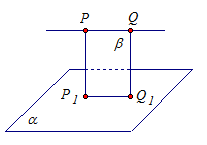
Рис. 5

Дано: ,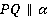

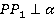
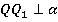
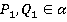
Доказать: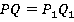

Доказательство:

Две прямые РР₁ и QQ₁ перпендикулярны к одной и той же плоскости α. Значит, эти прямые параллельны между собой. Пусть через них проходит плоскость β. В плоскости β прямые PQ и P₁Q₁ параллельны, так как по условию PQ параллельна α.

Рассмотрим прямоугольник РР₁Q₁Q.

В прямоугольнике РР₁Q₁Q противоположные стороны равны, значит, PQ = P₁Q₁, что и требовалось доказать.

Задача 2Через точки P и Q прямой PQ проведены прямые, перпендикулярные плоскости α и пересекающие ее соответственно в точках P₁ и Q₁.(рис.6)

Найдите P₁Q₁, если PQ = 15см., РР₁= 21,5 см., QQ₁= 33,5 см.

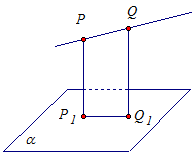
Рис. 6

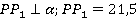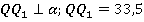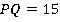Дано: см

см

Найти: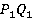

Решение:

Две прямые РР₁ и QQ₁ перпендикулярны к одной и той же плоскости α. Значит, прямые РР₁ и QQ₁ параллельны. Значит, через них проходит единственная плоскость PQQ₁P₁. Прямая РР₁ перпендикулярная плоскости α, а значит и прямой Р₁Q₁. Так как прямые РР₁ и QQ₁ параллельны, а угол РР₁Q₁ прямой, то четырехугольник РР₁Q₁Q - прямоугольная трапеция.

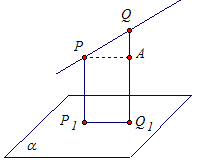
Рис. 7

Проведем прямую РА перпендикулярно прямой QQ₁.Отрезки РА и P₁Q₁ равны.

Отрезок Q₁A равен отрезку РР₁. Найдем QA: QA = QQ₁ - АQ₁ = QQ₁ - РР₁ = 33,5 - 21,5 = 12 см.

Рассмотрим треугольник АРQ. Он прямоугольный, так как угол QАР прямой. Найдем катет РА.

см.

P₁Q₁ = РА = 9 см.

Ответ: 9 см.

Домашнее задание:

Составьте опорный конспект