Написать конспект

2. Написать конспект

Параллелепипедом называется призма, основанием которой служит параллелограмм.

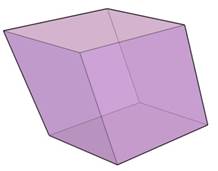
Стороны параллелограмма называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда.

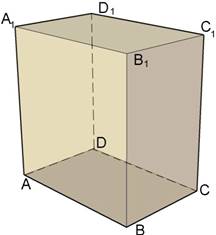
A, B, C, D, A₁, B₁, C₁, D₁ – вершины параллелепипеда.

АА₁, ВВ₁, СС₁, DD₁ – боковые ребра параллелепипеда.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. А и А₁ – противолежащие вершины.

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. ABCD и A₁B₁C₁D₁ – противолежащие грани.

Две грани параллелепипеда имеющие общее ребро называются смежными. АВВ₁А₁ и ВСС₁В₁ – смежные грани.

Параллелепипед, боковые ребра которого перпендикулярны основаниям, называется прямым. У прямого параллелепипеда боковые грани – прямоугольники.

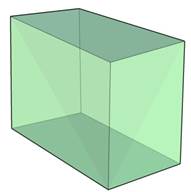
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным.

Всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой параллелепипед есть прямоугольный. Основанием прямого параллелепипеда может служить параллелограмм, не являющийся прямоугольником.

Куб - это прямой параллелепипед, все грани которого являются равными квадратами.

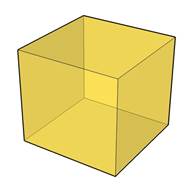
Длины трех ребер, выходящих из одной вершины, называются измерениями прямоугольного параллелепипеда.

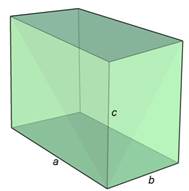
Параллелепипед, боковые ребра которого не перпендикулярны к основаниям, называется наклонным.

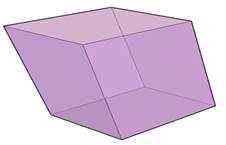
Отрезок, соединяющий противолежащие вершины параллелепипеда, называются диагональю параллелепипеда.

СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА:

1) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

2) У параллелепипеда противоположные грани параллельны и равны

3) В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений: d²=a²+b²+c²

Площадь полной поверхности прямоугольного параллелепипеда равна:

S_п = 2 (ab + bc + ac)

Площадь полной поверхности куба равна:

S_п= 6 a²

⇐ Предыдущая 12