
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уважаемый студент, добрый день.
Уважаемый студент, добрый день.
В тетрадь записываем число и свою фамилию собственноручно!
Решения с ответами прислать на на e-mail: altjin46@rambler.ru или в личку ВК.
Изучение новой темы
Тема: Показательные неравенства(записать в тетрадь)
Определение. Показательные неравенства - это неравенства вида ax > ay (ax < ay), где основание а- положительное число, неравное 1, и неравенства, сводящиеся к этому виду.
Такие неравенства решаются с помощью свойств монотонности показательной функции.
1. ax > ay , если a > 1, то показательное неравенство равносильно неравенству
x > y.
Аналогично, если ax < ay, то x < y
2. ax > ay, если 0 < a < 1, то показательное неравенство равносильно неравенству x < y.
Аналогично, если ax < ay, то x > y.
I Способ: приведение обеих частей к одному и тому же основанию.
Задания с решениями и ответами записать в тетрадь
Решить неравенство
№ 1. 3х>9
Решение: приводим 9 к основанию 3
3х > 32
т. к. основание 3 > 0, то по свойству 1. x > 2
Ответ: x > 2
№ 2. 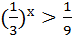
Решение: приводим  к основанию
к основанию 
 т. к. основание
т. к. основание 
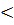 1, то по свойству 2. x
1, то по свойству 2. x 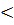 2
2
Ответ: x 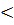 2
2
II Способ: неравенства, сводящиеся к квадратным
Задания с решениями и ответами записать в тетрадь
Решить неравенство
№ 3. 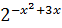 < 4
< 4
Решение: 4 приводим к основанию 2
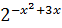 < 22 (по 1 способу основание 2>1, значит знак между показателями будет этот, не меняется)
< 22 (по 1 способу основание 2>1, значит знак между показателями будет этот, не меняется)
-x2+3x < 2
-x2+3x-2 < 0, получилось квадратное неравенство, приравниваем к 0
-x2+3x-2 = 0 - квадратное уравнение решаем через дискриминант. получаем
х1=1, х2=2
строим луч Ох, указываем точки х1=1, х2=2 и определяем знаки на интервалах.
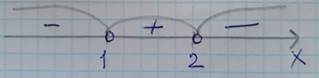
Ответ: (- 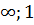 )
) 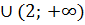
III Способ: вынесение общего множителя за скобки.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|