
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Самостоятельная работа
- Выполните размещённую после теоретического материала с примерами решения самостоятельную работу. - Выполненное домашнее задание можно направлять на мою электронную почту или в контакте, можно в виде фото листа тетради. Степанова Л.В.-адрес электронной почты: lora01051966@mail.ru
- Рассмотрите примеры решения методом интервалов.
- Чтобы применять метод интервалов, неравенство должно иметь вид – в левой части неравенства произведение нескольких множителей, в правой части неравенства 0. При необходимости неравенства приводим к такому виду, переносим всё в левую часть из правой части , чтобы там был 0, а левую часть раскладываем на множители любым из известных нам способом (выносим общий множитель за скобки, применяем формулы сокращённого умножения и т.д.).
№1. (6+х)(3х-1)≤0 Решаем, используя алгоритм:
во втором двучлене можно вынести 3 за скобки:
3 (х+6)(х-⅓)≤0, выделим функцию
φ(х)=3(х+6)(х-⅓)
1). Найдём D(φ) = R (область определения)
2).Нули функции 3(х+6)(х-⅓)=0 (значения х, при которых множитель = 0)
х1 =-6; х2 =⅓ (так как неравенство нестрогое, точки отмечаем закрашенные),
+ -6 - 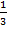 +
+


 3) х є [-6; ⅓] определяем знак функции на крайнем справа промежутке, это +, дальше чередуем знаки – и +. Чтобы определить знак функции на промежутке, берём из него любое число, подставляем в произведение 3(х+6)(х-⅓) вместо х. Нужно просто определить знак произведения. Так как в исходном неравенстве знак
3) х є [-6; ⅓] определяем знак функции на крайнем справа промежутке, это +, дальше чередуем знаки – и +. Чтобы определить знак функции на промежутке, берём из него любое число, подставляем в произведение 3(х+6)(х-⅓) вместо х. Нужно просто определить знак произведения. Так как в исходном неравенстве знак 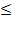 , в ответ записываем промежуток на котором стоит знак -.
, в ответ записываем промежуток на котором стоит знак -.
Ответ: [-6; ⅓]
№ 2. у= 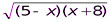
Область определения данной функции вытекает из условий, что подкоренное выражение должно быть неотрицательным, та как корень чётной степени, т.е. (5-х)(х+8) 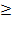 0
0
Решим неравенство, используя алгоритм.
(5 - х)(х+8) 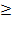 0, выделим функцию
0, выделим функцию
φ(х) = (5 - х)(х+8)
1). D(φ) = R
2).Нули функции (5 - х)(х+8) =0
х1 =5; х2 =-8 неравенство нестрогое, значит отмечаем две закрашенные точки


 - -8 + -
- -8 + -
 5
5
х є [-8; 5] Определяем знак произведения (5 - х)(х+8) на крайнем справа промежутке, это -, дальше чередуем справа налево + ,потом -. В ответ выбираем промежуток с +, так как знак неравенства 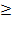 .
.
область определения данной функции: [-8; 5]
Ответ: [-8; 5]
№3.
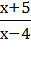
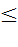 0 На 0 делить нельзя, поэтому область определения функции х
0 На 0 делить нельзя, поэтому область определения функции х 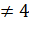 , так как х-4
, так как х-4 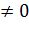
Нули функции х= - 5, х=4. Знак неравенства нестрогий точка -5 закрашенная, точка 4 пустая. Берём крайний справа промежуток, определяем знак дроби 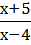 на этом промежутке, это +, далее на промежутках чередуем знаки -, потом +.
на этом промежутке, это +, далее на промежутках чередуем знаки -, потом +.


 + -5 - 4 +
+ -5 - 4 +
в исходном неравенстве знак 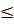 , значит в ответ берём промежуток, на котором знак -.Ответ: -5
, значит в ответ берём промежуток, на котором знак -.Ответ: -5 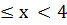 .( или
.( или 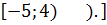
- Рассмотрев приведённые примеры, решить неравенства методом интервалов:
Самостоятельная работа
1) Решите неравенство:
а) (х-1)(х-3)>0
б) (х+3)(х-8)(х-20)≤0
в) 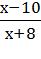 >0
>0
2) Найдите область определения функции:
а) у= 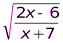
б) у= 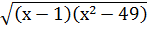
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|