
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Итоговая работа по математике за курс основной школы
20 мая
Итоговая работа по математике за курс основной школы
2019 - 2020 учебный год
1.Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Диван | Письменный стол | Журнальный столик | Торшер |
| Цифры |
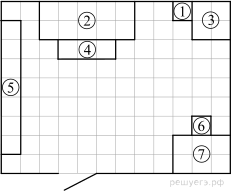
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен письменный стол, а к нему приставлен стул, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик. Площадь, занятая диваном, по плану будет равна 1,6 м2. В оставшемся свободным углу планируется поставить кресло. Слева от кресла будет стоять торшер. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 5 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло и диван.
2.Паркетная доска продаётся в упаковках по 26 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол в гостиной?
3.Найдите площадь той части гостиной, на которой не будет смонтирован электрический подогрев пола. Ответ дайте в м2.
4.Найдите расстояние от журнального столика до стула (расстояние между двумя ближайшими точками по прямой) в метрах.
5.В гостиной предполагалось класть ламинат, но решили не экономить и покрыть пол паркетной доской. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое количество м2 материала. Сколько рублей можно было бы сэкономить сэкономить, если бы владелец решил покрыть пол ламинатом?
| Тип покрытия | Стоимость 0,16 м2 материала (руб.) | Стоимость укладки 0,16 м2 материала (руб.) | Количество материала в упаковке (м2) |
| Паркетная доска | 0,64 | ||
| Ламинат | 0,48 |

6.Вычислите: 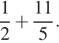
7.На координатной прямой отмечены числа 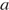 и
и 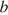 :
:

Какое из следующих чисел наибольшее?
1) 
2) 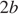
3) 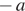
4) 
8.Расположите в порядке возрастания числа: 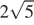 ;
; 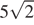 ; 6.
; 6.
В ответе укажите номер правильного варианта.
1) 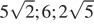
2) 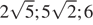
3) 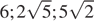
4) 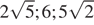
9.Найдите корни уравнения  .
.
Если корней несколько, запишите их в ответ без пробелов в порядке убывания
10.На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Параллелограмм», равна 0,2. Вероятность того, что это окажется задача по теме «Площадь», равна 0,1. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику не достанется задача ни по одной из этих двух тем.
11.Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 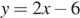
Б) 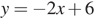
В) 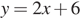
ГРАФИКИ
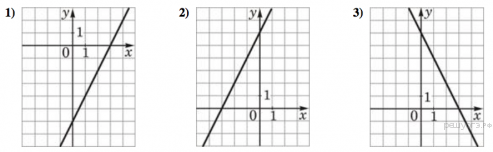
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
12.Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = - 8,7. Найдите a9.
13.Найдите значение выражения 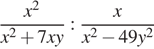 при
при 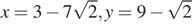
14.Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 255° по шкале Фаренгейта? Ответ округлите до десятых.
15.Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) x2 − 15 < 0
2 ) x2 − 15 > 0
3) x2 + 15 < 0
4 ) x2 + 15 > 0
16.
Точки А и B являются серединами сторон MN и NK треугольника MNK, сторона MN равна 52, сторона NK равна 78, сторона MK равна 96. Найдите AB
17. 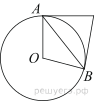
Касательные в точках  и
и 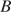 к окружности с центром в точке
к окружности с центром в точке 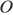 пересекаются под углом 86°. Найдите угол
пересекаются под углом 86°. Найдите угол 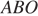 . Ответ дайте в градусах.
. Ответ дайте в градусах.
18.  Периметр равнобедренного треугольника равен 176, а боковая сторона — 55. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 176, а боковая сторона — 55. Найдите площадь треугольника.
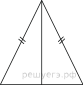
19. 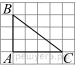 Найдите синуc угла B треугольника ABC , изображённого на рисунке.
Найдите синуc угла B треугольника ABC , изображённого на рисунке.
20.Какие из следующих утверждений верны?
1) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Около всякого треугольника можно описать не более одной окружности.
Если утверждений несколько, запишите их номера в порядке возрастания.
21.Решите уравнение 2х3 + 6х2 = 24 + 16х
22.Из пункта А в пункт Б, расстояние между которыми 420 километров отправляются одновременно автомобилисты Иванов и Степанов. Степанов едет со скоростью, на 24 км/ч большей, чем Иванов, и прибывает к финишу на 2 ч раньше второго. Найдите скорость Иванова автомобиля.
23.Постройте график функции у= │5 - 6х+ х2│ наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
24.Отрезки МК и DC лежат на параллельных прямых, а отрезки МC и КD пересекаются в точке Е. Найдите ЕC, если МК = 15, DC = 30, МC = 39 .
25.Известно, что около четырёхугольника PKFD можно описать окружность и что продолжения сторон PD и KF четырёхугольника пересекаются в точке M. Докажите, что треугольники MPK и MFD подобны.
26.Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|