
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Письменная экзаменационная работа
Письменная экзаменационная работа
Время выполнения: 6 академических часов.
Вариант 4
Обязательная часть
B1. (1 балл) На автозаправке клиент отдал кассиру 2000 рублей и залил в бак 28 литров бензина по цене 40 руб. 50 коп. за литр. Сколько рублей сдачи он должен получить у кассира?
B2. (1 балл) На рисунке жирными точками показана среднесуточная температура воздуха каждый день с 4 по 19 января 2019 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией.

Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.
B3. (1 балл) На клетчатой бумаге с клетками размером 1 см × 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
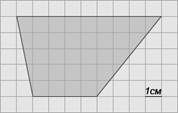
B4. (1 балл) Петя бросает игральный кубик. С какой вероятностью на верхней грани выпадет четное число?
B5. (1 балл) Решите уравнение: 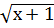 = 5.
= 5.
B6. (1 балл) В прямоугольном треугольнике АВС катеты равны 15 и 6. Найдите тангенс острого угла при большем катете.
B7. (1 балл) Тело движется по закону: S(t) = t2-5t+3. Определите, в какой момент времени скорость будет равна 7.
B8. (1 балл) Рёбра прямоугольного параллелепипеда равны 4, 7 и 4. Найдите диагональ.
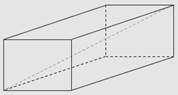
B9. (1 балл) Найдите значение выражения 3926:66
B10. (1 балл) Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 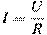 , где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 25 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 В, чтобы сеть продолжала работать. Ответ выразите в Омах.
, где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 25 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 В, чтобы сеть продолжала работать. Ответ выразите в Омах.
B11. (1 балл) Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
B12. (2 балла) На отрезке [9;13] найдите наименьшее значение функции f(x)=x3−20x2+100x+23.
B13. (2 балла) Решите уравнение: 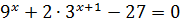
B14. (2 балла) Решите неравенство: 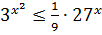
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|