
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Домашнее задание: 0.1гл.2§.11упр 11.19 стр.306
Примеры.
1.Решить неравенство cos x 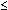 1/2.
1/2.
Решение: Абсциссу, не большую 1/2, имеют все точки дуги М1ММ2 единичной окружности (см. рисунок).
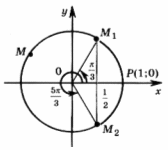
Поэтому решениями неравенства cos x 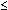 1/2 являются числа х, принадлежащие промежутку
1/2 являются числа х, принадлежащие промежутку  /3
/3 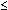 х
х 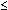 5
5  /3. Все решения данного неравенства – множество отрезков [
/3. Все решения данного неравенства – множество отрезков [  /3 +2
/3 +2  n ; 5
n ; 5  /3+2
/3+2  n ], n
n ], n  Z.
Z.
Ответ: [  /3 +2
/3 +2  n ; 5
n ; 5  /3+2
/3+2  n ], n
n ], n  Z.
Z.
2.Решить неравенство tg x > 1.
Решение: Построим графики функций у = tg x и у = 1.
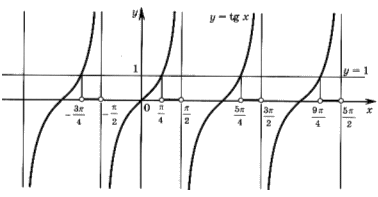
Рисунок показывает, что график функции у = tg x лежит выше прямой у=1 на промежутке (  /4;
/4;  /2), а также на промежутках, полученных сдвигами его на
/2), а также на промежутках, полученных сдвигами его на  n, где n
n, где n  Z.
Z.
Ответ: (  /4+
/4+  n ;
n ;  /2 +
/2 +  n ), где n
n ), где n  Z.
Z.
Домашнее задание: 0.1гл.2§.11упр 11.19 стр.306
С.р.№ 16
Решите тригонометрические уравнения:
а) sin2xcosx-3sin2x=0
b) cos2x+cosx=0
Решите тригонометрические неравенства:
а) tg2x 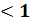
b)sin2x - 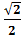 sinx
sinx 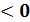
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|