Обобщение теоретического материала.

Урок 146 дата 05.06.20

Тема повторение Решение задач по теме Логарифмическая функция

Студенты отвечают так: "да" - V, "нет" - _.

Текст. Предлагаются верные и не верные утверждения.

Верны ли утверждения?

1. Логарифмическая функция у = log_ax определена при любом х.

2. Функция у = log 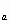x логарифмическая при а>0, а 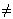1, х>0.

3. Область определения логарифмической функции множество действительных чисел.

4. Область значений логарифмической функции множество действительных чисел.

5. Логарифмическая функция является четной функцией.

6. Функция у = log₃x является возрастающей.

7. Функция у = log_ax при положительном а, но меньшим 1, является возрастающей.

8. Логарифмическая функция имеет экстремумы.

9. График функции у = log_ax пересекает ось Ох.

10. График логарифмической функции симметричен относительно оси Ох.

11. График логарифмической функции расположен в _ и _ V четвертях.

12. График логарифмической функции всегда пересекает ось Ох в точке (1,0).

Выполнение данного задания позволит проверить учащимся теоретический материал по теме свойства логарифмической функции.

момент.

3. Обобщение теоретического материала.

Функция вида у = log_ax называется логарифмической функцией с

Основанием а ( а>0, а 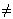1)

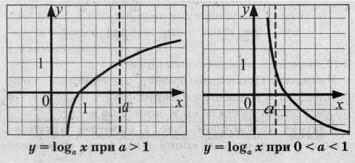
- область определения - множество всех положительных чисел (х>0).

- область значений - множество всех действительных чисел ( - ; + ).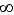

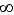- непрерывна на всей области определения.

- функция у = log 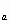x возрастает на всей области определения, если а>1.

- Функция у = log 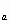x убывает на всей области определения, если 0< а>1.

- точка пересечения графика функции у = log_ax с осью Ох (1,0).

- наибольшего и наименьшего значения функции не существует.

- функция экстремумы не имеет.

- положение точки а относительно1, и значения функции при х=а

Пример: 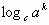=k log_c a , log_aa =1 log₂2³=3 log₂2=3,

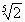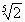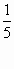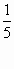log_c(ab)= log_ca + logb log₂2 = log₂2 + log₂ =1+ =1 =1,2.

log_ba= 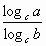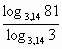=log₃81=4. и т.д.

Повторить

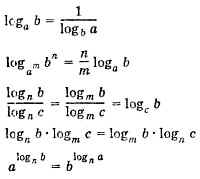
"Простейшее логарифмическое уравнение - это уравнение вида log_a x=b, где a 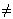0, а 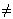1.Имеет единственное решение х= a^b.

a) log₃x=4, x>0, x=81,

b) log₂(x+1)=3, x>-1, x+1=8, x=7,

в) log_a16=2, а>0, а 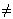1, а=4.

Решить по учебнику Ш.А.Алимов Алгебра и начало математического анализа 10-11 класс

№з68-372 под цифрой (1)379,380 (1)

Ответы отправить на почту mathetuka@yandex.ru

Тема:Тригонометрические формулы

Повторить

Определения синуса, косинуса, тангенса и котангенса.

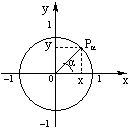
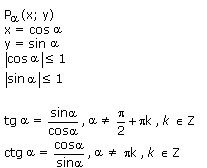
Основные тождества:

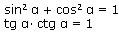
Знаки тригонометрических функций:

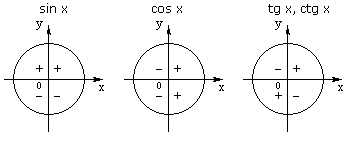
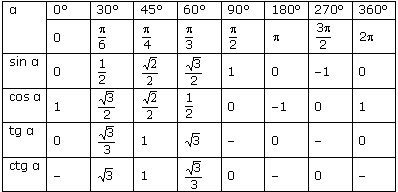
Значения тригонометрических функций

Формулы синуса, косинуса, тангенса и котангенса угла (–α):

sin (–α) = – sin α
cos (–α) = cos α
tg (–α) = – tg α
ctg (–α) = – ctg α

Формулы приведения:

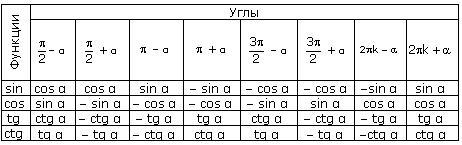
Все формулы приведения можно получить, пользуясь следующими правилами:
1. В правой части формулы ставится тот знак, который имеет левая часть при условии

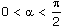
Решить по учебнику Ш.А.Алимов Алгебра и начало математического анализа 10-11 класс

Решить 546,547,548 под цифрой 1

Ответы отправить на почту mathetuka@yandex.ru