Примеры и разборы решения заданий тренировочного модуля

Урок 131 дата 14.05

Тема Четность и периодичность функцииТеоретический материал для самостоятельного изучения

Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |ОА| к длине гипотенузы |ОВ|.

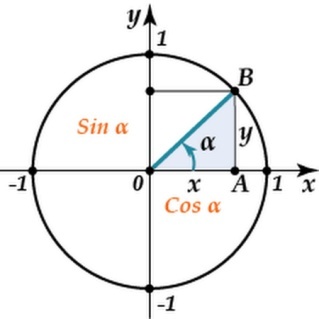
Область. определения функции (D) — множество R всех действительных чисел

Множество значений функции (E) — отрезок [-1; 1], т.е. косинус функция —ограниченная.

Для того, чтобы определить чётность функции косинус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).

Например, cos(60°) = ½ = cos(–60°)–это значит, что : cos(−x)=cos x для всех x∈R и у=сosx–чётная

Сиинус(sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |АВ| к длине гипотенузы |ОВ|.

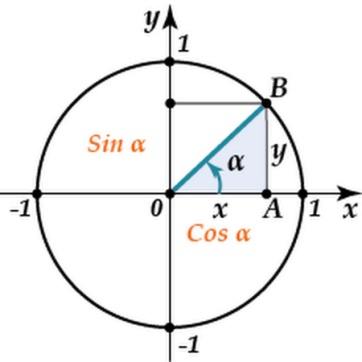
Область определения функции (D) — множество R всех действительных чисел.

Множество значений функции (E) — отрезок [-1; 1], т.е. синус функция —ограниченная.

Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).

Например, sin(30°) = ½ sin(–30°) = –½ –это значит, что : sin(−x)=–sin (x) для всех x∈R и y=sinx–нечётная

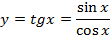
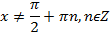
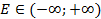
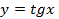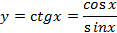
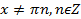
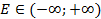
–нечётная

–нечётная

Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π.

Примеры и разборы решения заданий тренировочного модуля

Пример 1. Выясним, является ли функция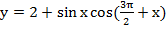

чётной или нечётной?

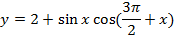
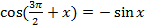
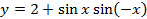
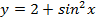
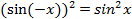
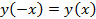
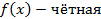
Пример 2.Доказать, что число 2π является наименьшим положительным периодом функции y=cos x

Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2πзакрепить посмотрев видео в yotube Четность, нечетность и периодичность тригонометрических функций. Алгебра 10-11 классы. 2 урок

Разобрать примеры и подобные решить по учебнику Ш.А.Алимов Алгебра и начало математического анализа 10-11 класс

Домашняя работа №700.701.702

Ответы отправить на почту mathetuka@yandex.ru

Не забывайте указывать в своих ответах номер урока, свою фамилию и дату урока. Ответы на один урок отправлять одним файлом!!!!!!!!