
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок № 49. Системы тригонометрических уравнений.
Урок № 49. Системы тригонометрических уравнений.
Глоссарий по теме
Система уравнений– это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Записывается с помощью знака {
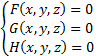 – система из трех уравнений с тремя неизвестными.
– система из трех уравнений с тремя неизвестными.
Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений обращается в верное равенство.
Теоретический материал для самостоятельного изучения
Основными методами решения систем уравнений являются:
- метод подстановки
- метод замены переменной.
Также при решении систем тригонометрических уравнений используются многие тригонометрические формулы.
Рассмотрим решение систем тригонометрических уравнений.
Пример 1.
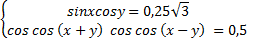
Решение:
При решении этой системы можно действовать по-разному:
1) можно использовать формулы преобразования произведения в сумму синусов (в первом уравнении) или косинусов (во втором уравнении)
2) можно использовать формулами косинуса суммы и разности во втором уравнении.
Воспользуемся формулой преобразования произведения косинусов в сумму косинусов:
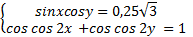 .
.
Теперь, учитывая, что косинус двойного аргумента может быть выражен через квадрат синуса и косинуса аргумента, возведем в квадрат первое уравнение. Но, так как возведение в квадрат не является равносильным преобразованием, введем ограничение:
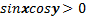 , то есть
, то есть 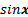 и
и 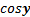 должны быть одного знака.
должны быть одного знака.
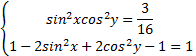 .
.
Теперь введем новые переменные:
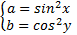 ,
, 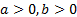 (*) и решим вспомогательную систему:
(*) и решим вспомогательную систему:
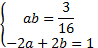 .
.
Решим ее методом подстановки.
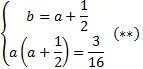 .
.
Решим уравнение (**).
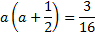
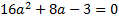
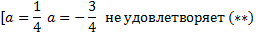 .
.
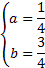 . Вернемся к исходным переменным.
. Вернемся к исходным переменным.
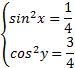 ,
,
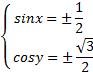 .
.
С учетом условия 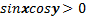 получим две системы:
получим две системы:
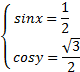
Или
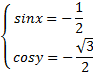
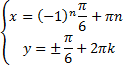
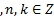 или
или
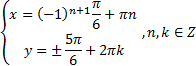
Ответ: 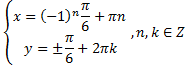
Или 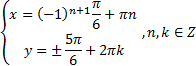
.
Рассмотрим еще один пример.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|