
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Нахождение значений у или х. Монотонность (промежутки возрастания и убывания). Экстремумы
2.Нахождение значений у или х
Смотрим по графику функции (как морской бой):
Если задан х = 2, то у для этой точки = 3.
Если х = -4, то у = -2.
И наоборот задания:
Если у = 1, то х = 0,5
Если у = 4, то х = 1
Если у = 3, то х = 0,8 и х = 2 (в таких случаях смотрите внимательно)
3. Монотонность (промежутки возрастания и убывания)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
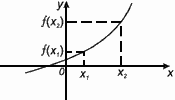 Промежутки возрастания (когда график идет вверх) определяют значения по оси Х, скобки квадратные.
Промежутки возрастания (когда график идет вверх) определяют значения по оси Х, скобки квадратные.
Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
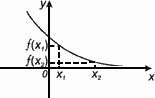 Промежутки убывания (когда график идет вниз) определяют значения по оси Х, скобки квадратные.
Промежутки убывания (когда график идет вниз) определяют значения по оси Х, скобки квадратные.
4. Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х) 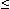 f(Xmax).
f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.
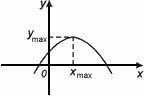
Хmax – точка максимума – (это х горики на графике)
Уmax – максимум функции – (это у горки)
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х) 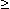 f(Xmin).
f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
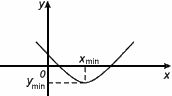
Xmin – точка минимума – (это х ямки на графике)
Ymin – минимум функции – (это у ямки)
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
5. Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
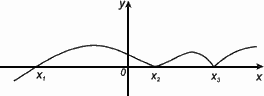
Х1,Х2,Х3 – нули функции y = f(x).
Нули функции – это точки пересечения графика с осью ОХ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|