
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа №2. Вариант 2. Решение.
Контрольная работа №2
Вариант 2
ЗАДАЧА 1. Дана функция двух переменных 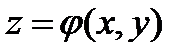 и точка D.
и точка D.
а) найти градиент функции 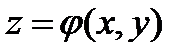 в точке D;
в точке D;
б) составить уравнение касательной плоскости и нормали к поверхности 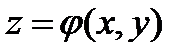 в точке D;
в точке D;
в) исследовать функцию 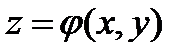 на экстремум.
на экстремум.
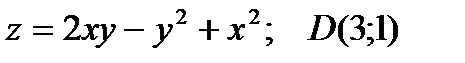
Решение.
а) Считая 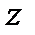 функцией одного аргумента
функцией одного аргумента 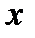 , находим,
, находим, 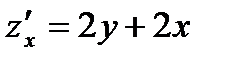
аналогично, считая 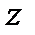 функцией одного аргумента
функцией одного аргумента 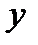 , находим,
, находим, 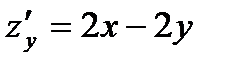 .
.
Затем вычисляем их частные производные в указанной точке: 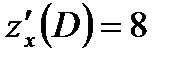
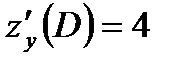 .
.
Применим формулу 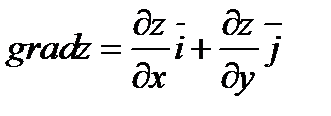
Градиент функции найдем по формуле:
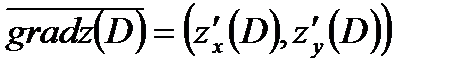 и получим
и получим 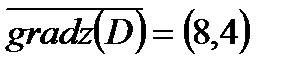 .
.
б) Преобразуя уравнение поверхности к виду 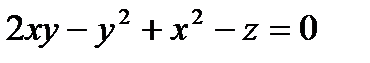 и обозначив его левую часть через
и обозначив его левую часть через 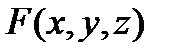 , найдем частные производные
, найдем частные производные 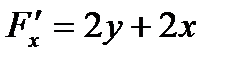 ,
, 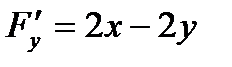 ,
, 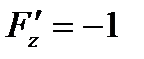 .
.
Вычислим их значения в данной точке 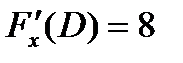 ,
, 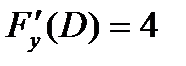 , и значение
, и значение 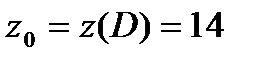 , затем применим формулу
, затем применим формулу
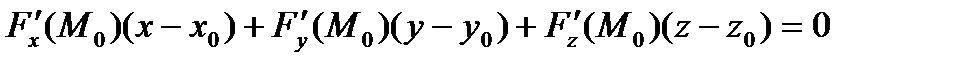
Получили уравнение касательной плоскости
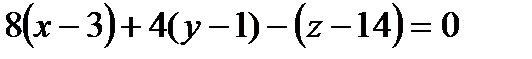 или
или
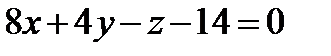
Уравнение нормали составим в виде
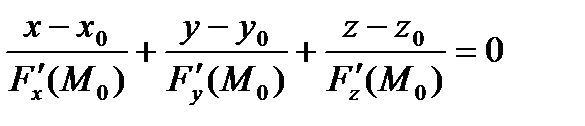
Находим окончательно
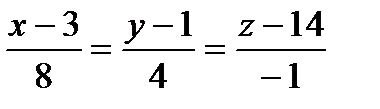
в) находим точки, в которых частные производные первого порядка 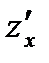
и 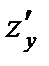 равны нулю или не существуют и которые лежат внутри области определения функции
равны нулю или не существуют и которые лежат внутри области определения функции
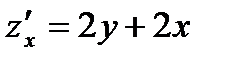 ,
, 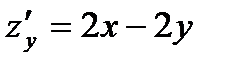 .
.
Решая систему уравнений
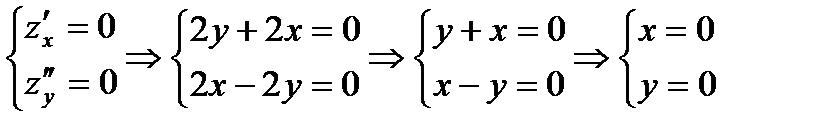
Находим точку М(0,0), которая является стационарной. Далее исследуем точки по знаку определителя  , составленного из частных производных второго порядка:
, составленного из частных производных второго порядка: 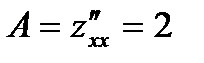 ,
, 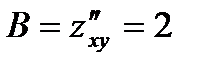 ,
, 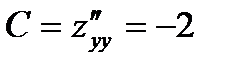 .
.
Для точки М получаем А=2, В=2, С=-2 и
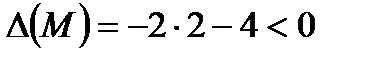 в точке М(0;0) экстремума нет.
в точке М(0;0) экстремума нет.
ЗАДАЧА 2. Найти неопределенные интегралы
а) 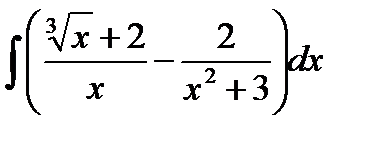 ;
;
б) 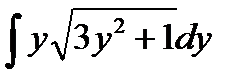 ;
;
в) 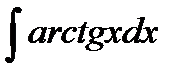 .
.
Решение.
а) 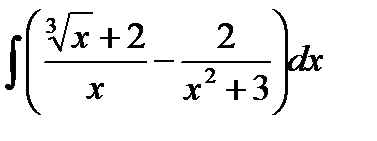
Используем метод непосредственного интегрирования.
Используем свойство линейности неопределенного интеграла. Это табличные интегралы.
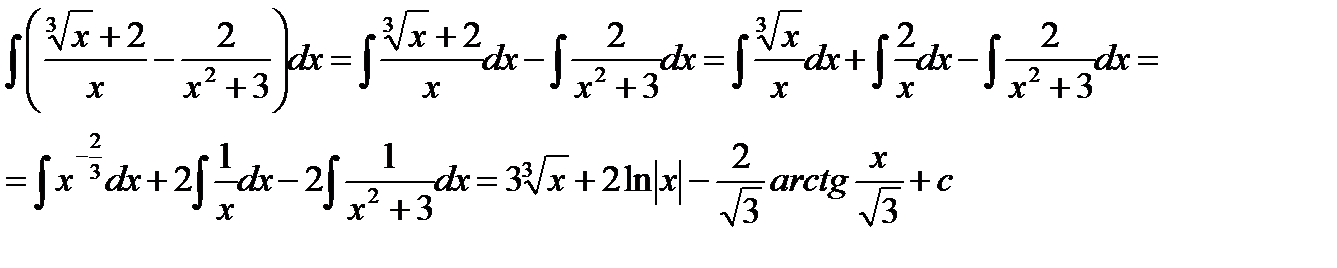
б) 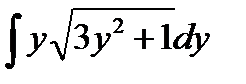
Используем метод замены переменной. Имеем интегралы вида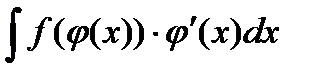 .Для сведения интеграла к табличному интегралу используем прямую подстановку
.Для сведения интеграла к табличному интегралу используем прямую подстановку 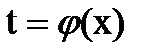 .
.
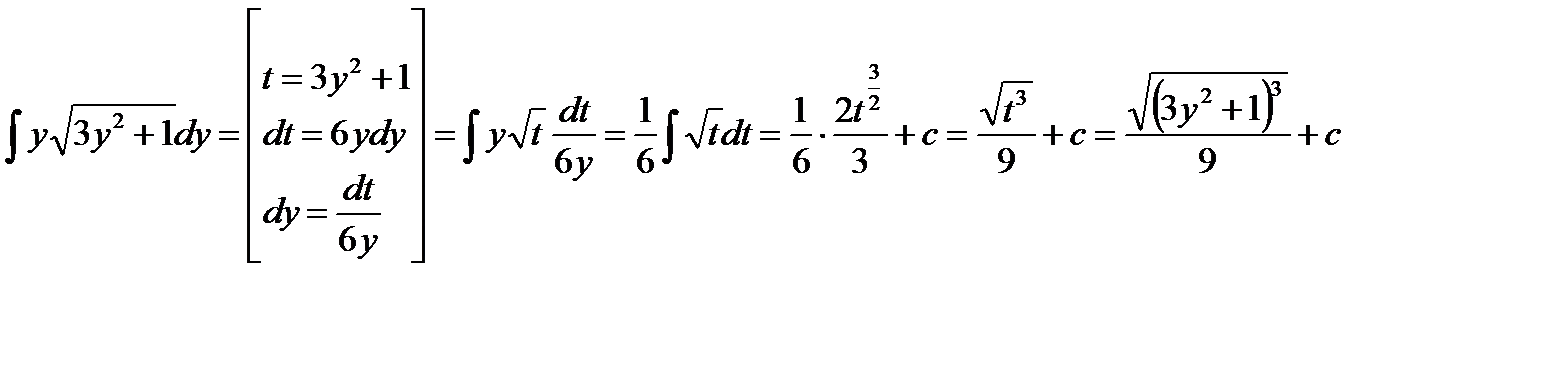
в) 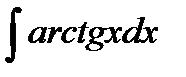
Применяем формулу интегрирования по частям: 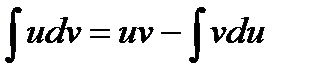 .
.
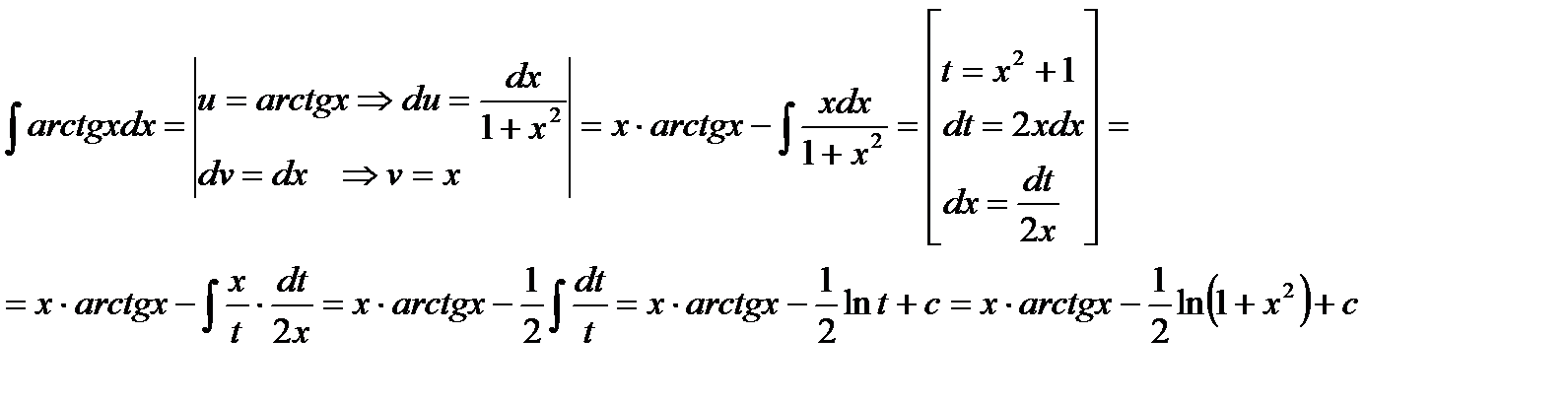
ЗАДАЧА 3. Вычислить определенные интегралы
а) 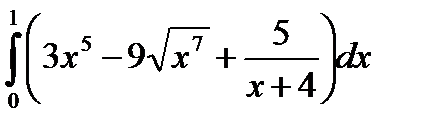
б) 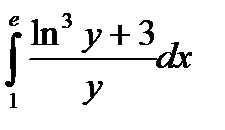
в) 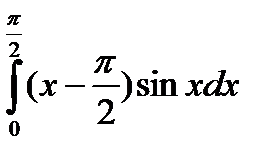
Решение.
а) 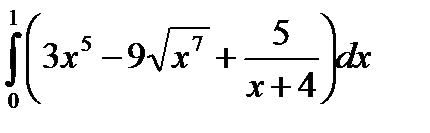
Используем формулу Ньютона-Лейбница.
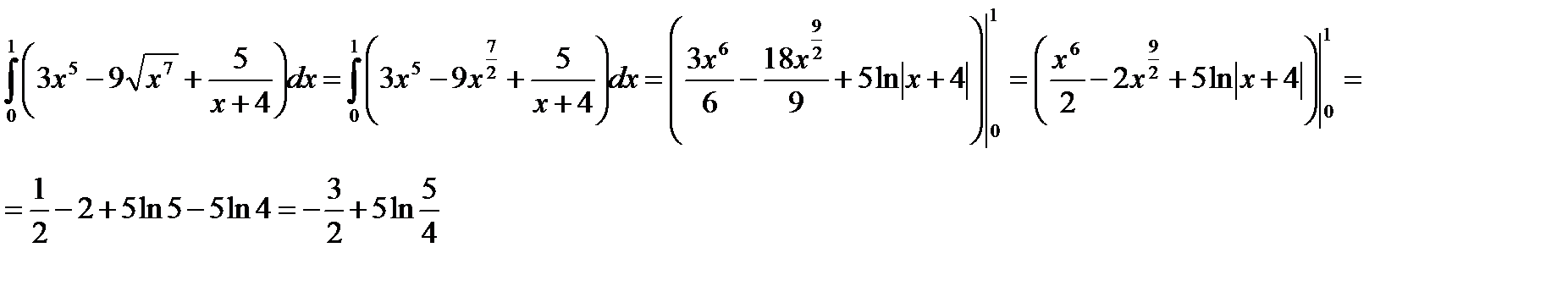
б) 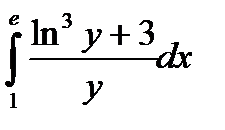
Используем метод замены переменной
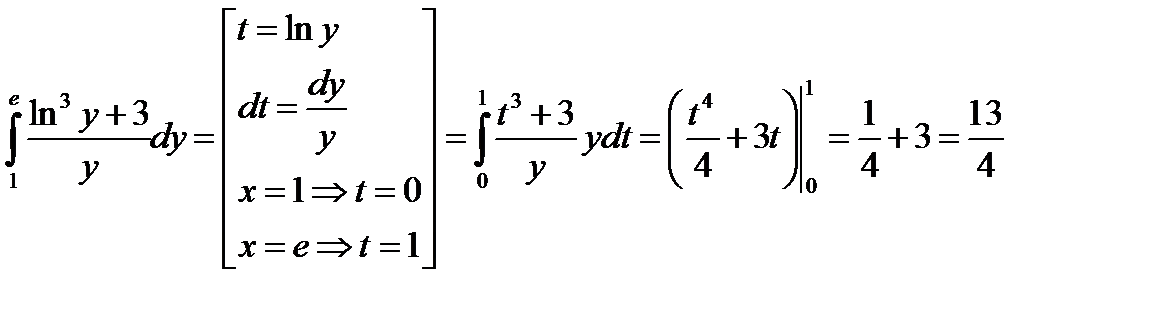
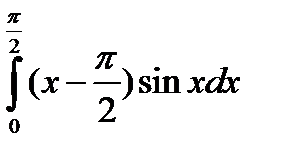 в)
в)
Испозьзуем формулу интегрирования по частям
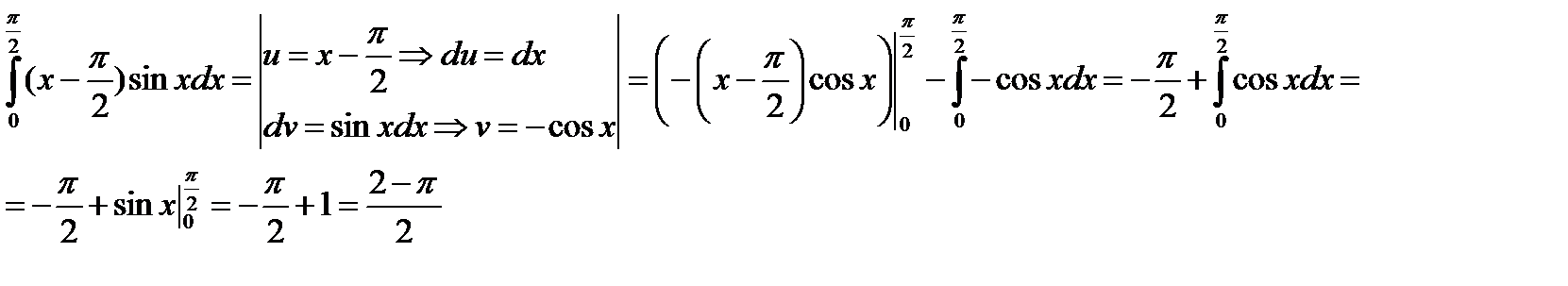
ЗАДАЧА 4. Определить площадь фигуры, ограниченной графиками данных функций:
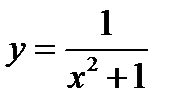 ,
, 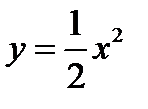 .
.
Решение.Строим графики функций.
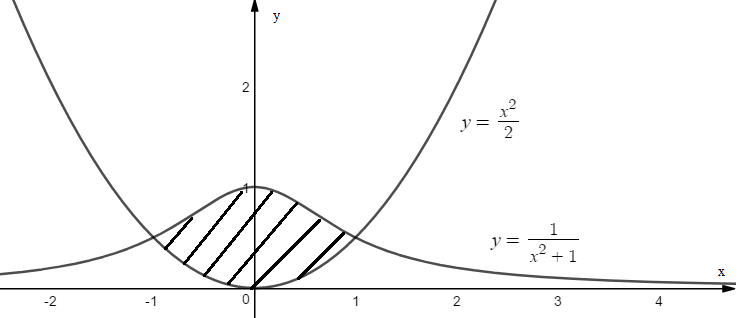
Затем для нахождения точек пересечения графиков решим систему уравнений
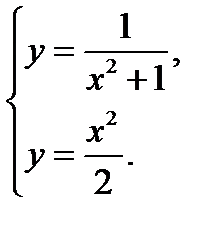
Приравнивая левые части, получим
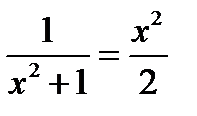 или
или 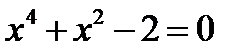
Пусть 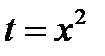 и
и 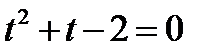
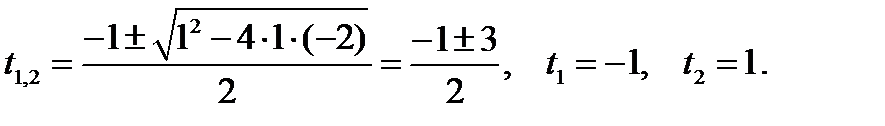
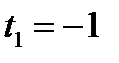 не является допустимым значением.
не является допустимым значением.
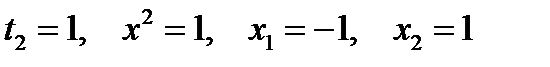
Тогда по формуле 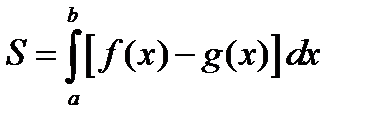 искомая площадь S будет равна:
искомая площадь S будет равна:
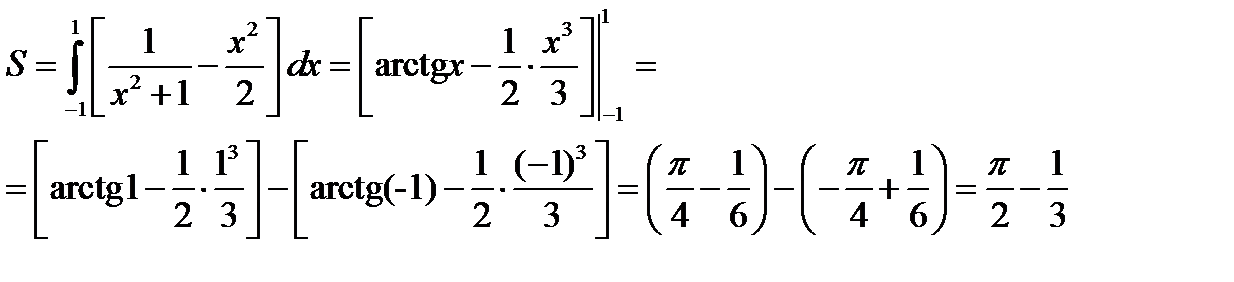
ЗАДАЧА 5.Решить дифференциальные уравнения первого порядка. В тех задачах, в которых заданы начальные условия, найти решения, удовлетворяющие этим условиям.
а) 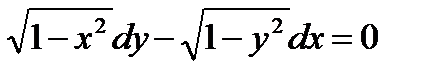
б) 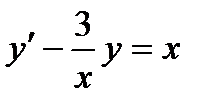 если
если 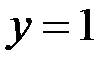 при
при 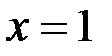 ;
;
Решение.
а) 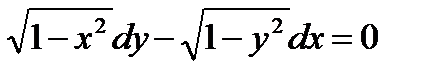 ;
;
Разделим переменные.
Разделим правую и левую части равенства на произведение множителей, стоящих не у своих дифференциалов:
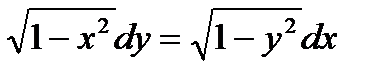 или
или 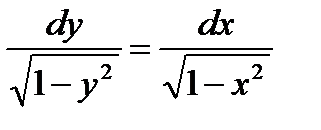
Проинтегрируем обе части последнего равенства: 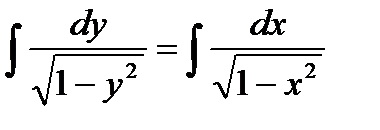 ,
,
Запишем решение
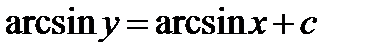
б) 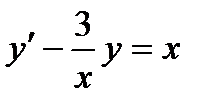 если
если 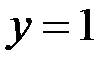 при
при 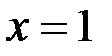 ;
;
Имеем линейное уравнение вида 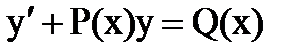 . Здесь
. Здесь 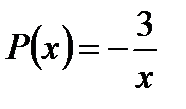 ,
,  .
.
Решим уравнение методом Бернулли. Положим 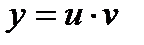 , откуда
, откуда 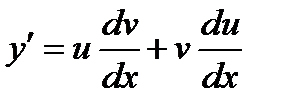 .
.
Подставим эти значения в уравнение : 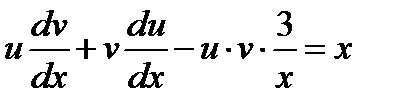 Сгруппируем члены, содержащие, например
Сгруппируем члены, содержащие, например 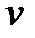 , и вынесем
, и вынесем 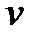 за скобку
за скобку 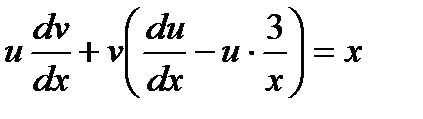 .
.
Выберем функцию 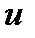 так, чтобы выражение в скобках обратилось в нуль. Тогда дифференциальное уравнение разобьется на два дифференциальных уравнения с разделяющимися переменными:
так, чтобы выражение в скобках обратилось в нуль. Тогда дифференциальное уравнение разобьется на два дифференциальных уравнения с разделяющимися переменными: 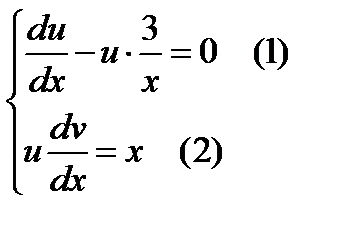
Решаем уравнение (1) при 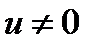 :
: 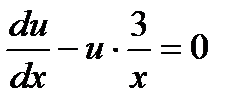 ,
, 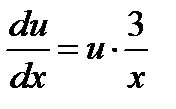 . Интегрируя почленно, имеем:
. Интегрируя почленно, имеем:
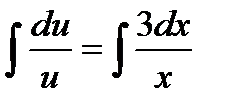 , или
, или 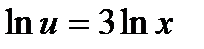 , или
, или 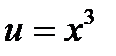 .Подставим это значение в уравнение (2):
.Подставим это значение в уравнение (2): 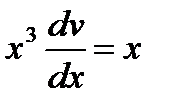 или
или 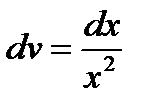 .
.
Интегрируя почленно, имеем: 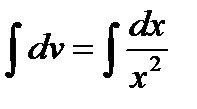 или
или 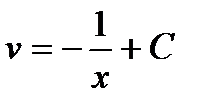 .
.
Заменив в подстановке 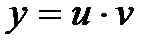 функции
функции 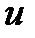 и
и 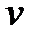 их выражениями из равенств (1) и (2), получим искомое общее решение данного уравнения:
их выражениями из равенств (1) и (2), получим искомое общее решение данного уравнения:
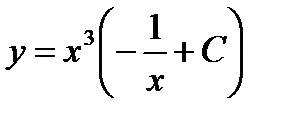 .
.
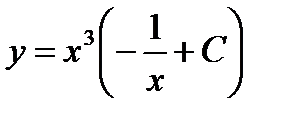 - общий интеграл данного уравнения.
- общий интеграл данного уравнения.
Удовлетворим начальные условия
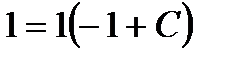
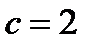
Запишем частное решение
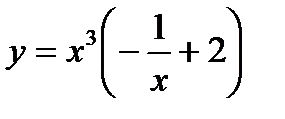
ЗАДАЧА 6. Найти решение однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами. В тех задачах, в которых заданы начальные условия, найти решения, удовлетворяющие этим условиям.
а) 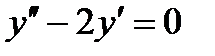 , если
, если 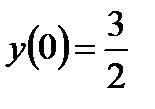 ,
, 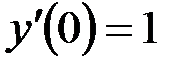 ;
;
б) 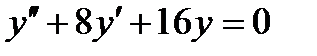 ;
;
в) 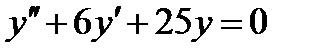 .
.
Решение.
а) 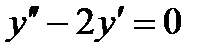 , если
, если 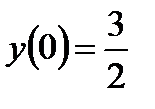 ,
, 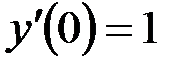 ;
;
Ищем общее решение уравнения в виде 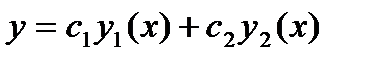 , где
, где 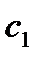 и
и 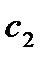 - произвольные постоянные,
- произвольные постоянные, 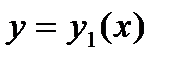 и
и 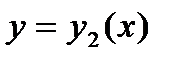 - частные линейно- независимые решения.
- частные линейно- независимые решения.
Запишем характеристическое уравнение
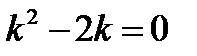
Найдем его корни.
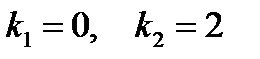
Корням соответствуют частные решения 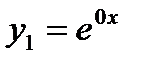 и
и 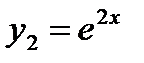 . Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид
. Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид 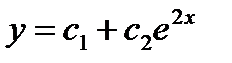 .
.
Для нахождения постоянных 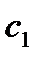 и
и 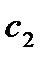 используем начальные условия
используем начальные условия 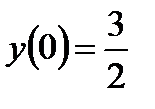 ,
, 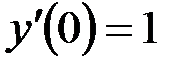
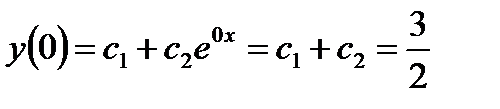
Чтобы использовать условие на производную, продифференцируем общее решение
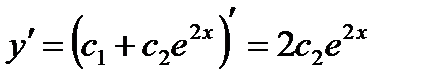
Теперь используем условие 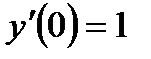 .
.
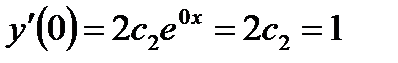
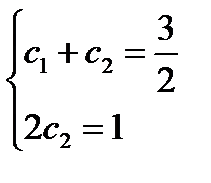 ,
, 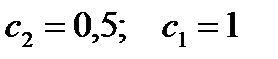
Тогда частное уравнение запишется так:
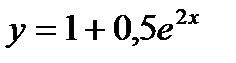
б) 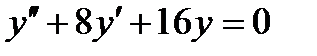 ;
;
Запишем характеристическое уравнение
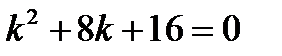
Найдем его корни
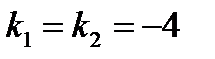 .
.
Корням соответствуют частные решения 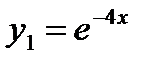 и
и 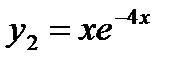 . Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид
. Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид 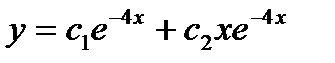
в) 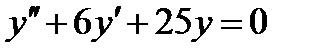
Запишем характеристическое уравнение
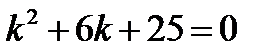
Найдем его корни
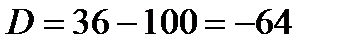 ,
, 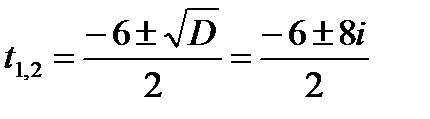
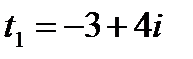 и
и 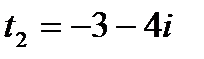 .
.
Корням соответствуют частные решения 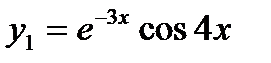 и
и 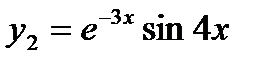 . Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид
. Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид 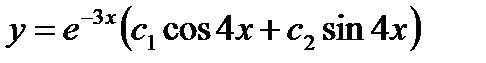
ЗАДАЧА 7. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами
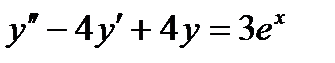
Решение.
Сначала найдем общее решение соответствующего однородного уравнения.
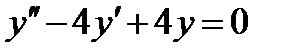 .
.
Запишем характеристическое уравнение
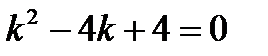
Найдем его корни. 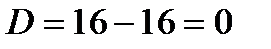 ,
, 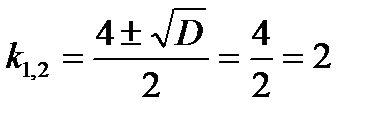
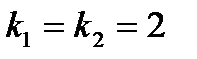 . Корням соответствуют частные решения
. Корням соответствуют частные решения 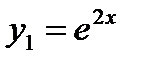 и
и 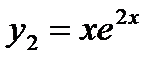 . Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид и
. Т.к. решения являются линейно независимыми функциями, то общее решение дифференциального уравнение имеет вид и 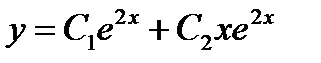
Теперь найдем частное решение неоднородного уравнения. По виду правой части частное решение неоднородного уравнения запишется
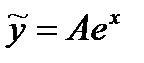 .
.
Найдём первую и вторую производную:
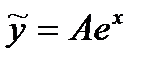
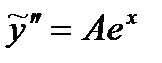
Подставим 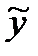 ,
, 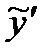 и
и 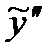 в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
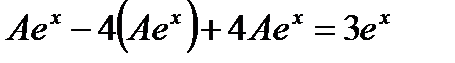
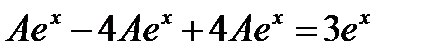
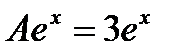
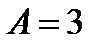
Тогда общее решение неоднородного уравнения запишется
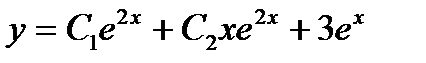
ЗАДАЧА 8. Вычислить двойной интеграл
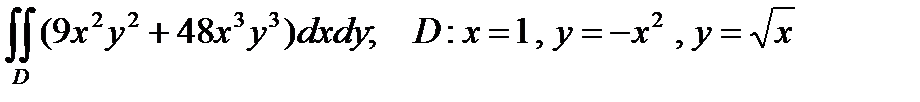 .
.
Строим область D
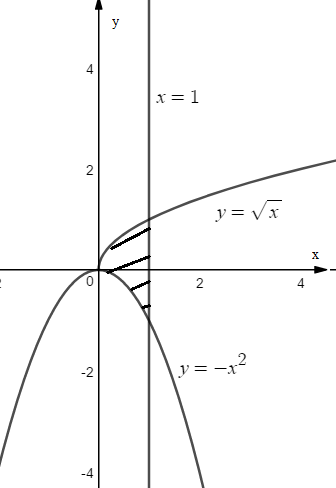
Из рисунка 5 делаем вывод, что область D ограничена сверху кривой 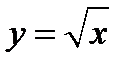 , снизу – кривой
, снизу – кривой 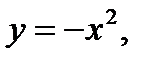 при любом фиксированном значении x из отрезка [0;1].
при любом фиксированном значении x из отрезка [0;1].
Поэтому имеем
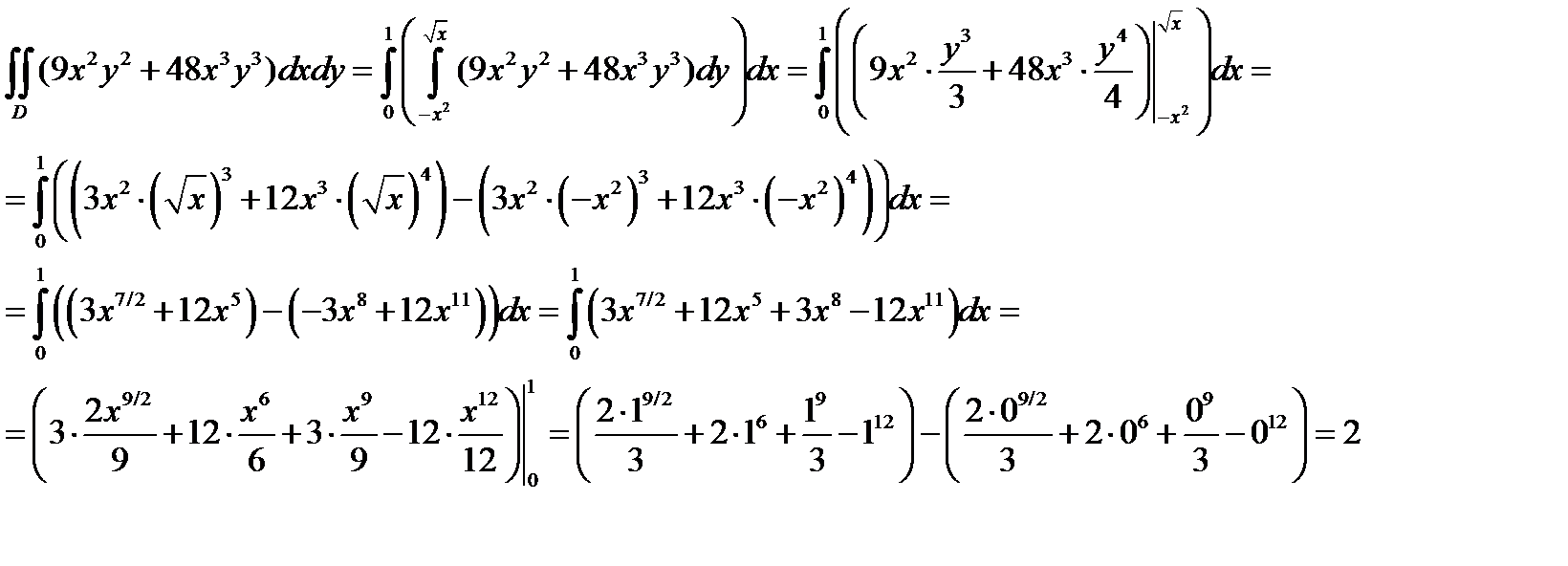
ЗАДАЧА 9.Представить комплексное число в тригонометрической форме
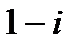
Решение.
Комплексное число в тригонометрической форме имеет вид
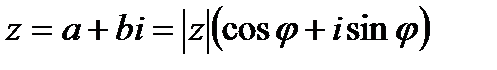 .
.
Найдем модуль и аргумент комплексного числа
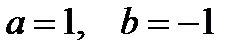 .
.
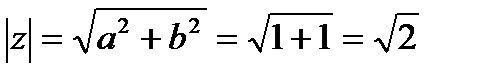
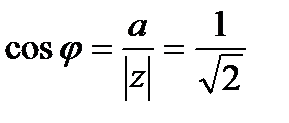
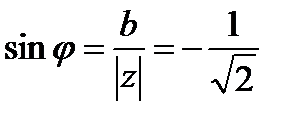 , тогда
, тогда 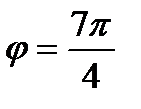
 Таким образом, число в тригонометрической форме имеет вид
Таким образом, число в тригонометрической форме имеет вид
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|