Объемы тел

Объемы тел

1. В прямоугольном параллелепипеде ABCDА₁ В₁ С₁ D₁площадь боковой грани A А₁ B₁B равна 60см², длина ребра AD равна 7см. Вычисли объём.

2. Куб, объём которого 27м³, распилили на кубики со стороной 2см и положили их в один ряд. Вырази длину получившегося ряда в сантиметрах.

3. 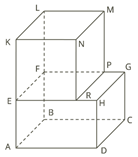Вычисли объём фигуры, которую образуют прямоугольные параллелепипеды ABCDEFGH и EFPRKLMN, если RN=9см; HD=9см; CB=12см; GP=2см; LK=12см.

4. Рёбра прямоугольного параллелепипеда относятся как a:b:c=1:7:3. Вычисли длину рёбер, если объём прямоугольного параллелепипеда равен 1344см³

5. В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=8см;AD=5см.

Площадь сечения, проходящего через середину ребра A1B1 и ребро CD, равна 8⋅ 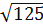см².Найдите объём

6. Сторона основания правильной треугольной призмы равна 8см, высота призмы равна 11 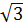см. Вычисли объём и площадь поверхности призмы.

7. Основанием прямой призмы является ромб, диагонали которого равны 6см и 8  см. Большее диагональное сечение призмы равно 72см². Вычисли объём призмы.

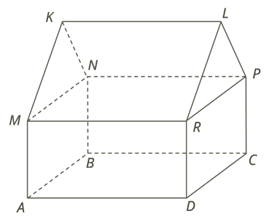
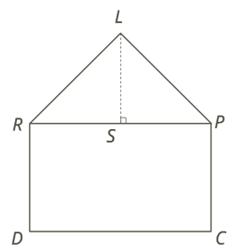
8. Вычислить объём сарая в кубических метрах. Все четырёхугольники на чертеже — прямоугольники, все треугольники — равнобедренные.

AD= 7,5 м; CD= 5,6 м; AM= 2,4 м; SL= 1,6 м.

9. Вокруг куба описан цилиндр. Ребро куба равно 12см. Вычисли объём цилиндра.

10. Сторона основания правильной шестиугольной призмы равна 4см, а высота равна 5 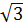см . Вычисли объём призмы.

11. Вычислить объём меньшего шарового сегмента, если высота сегмента равна 1,5см, а радиус шара равен 2,9см.

12. Шар с центром в точке O касается плоскости в точке A. Точка B лежит в плоскости касания. Найди объём шара, если AB=16,8см, а BO=23,2см. (Ответ округли до десятых!)

13. Радиусы оснований усечённого конуса соответственно равны 9 см и 8 см, а высота равна 12 см. Вычисли объём конуса.

14. Цинковый провод диаметром 2,2 мм имеет массу 1,9 кг. Вычисли длину провода, если плотность цинка 7,13 г/см³. Значение числа π в вычислениях округлить до 3. Результат округли до сантиметров.