
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определенные интегралы
Определенные интегралы
Несобственные интегралы 2 рода. Площади фигур.
| 9.2.1(10) | 
|
| 9.2.1(11) | Найти 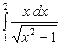 . Пусть . Пусть 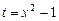 , , 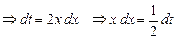 . .  . .
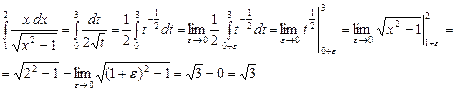
|
| 9.2.1(13) | 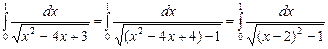 .
Пусть .
Пусть 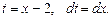 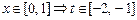 . Тогда: . Тогда:
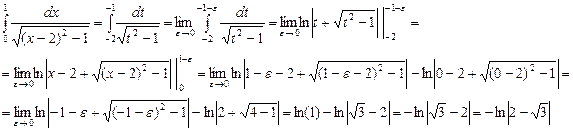
|
| 9.2.1(14) | 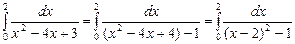 .
Пусть .
Пусть 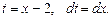 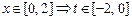 . Тогда . Тогда 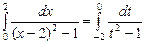 .
Функция .
Функция 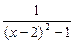 на отрезке [0, 2] терпит разрыв в точке х=1, а функция на отрезке [0, 2] терпит разрыв в точке х=1, а функция
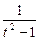 на отрезке [–2, 0] терпит разрыв в точке t = –1. Следовательно: на отрезке [–2, 0] терпит разрыв в точке t = –1. Следовательно:
 Т.о., интеграл расходится.
Т.о., интеграл расходится.
|
| 9.3.1(1) | 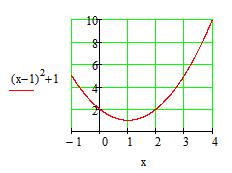 Вычислить площадь фигуры, ограниченной линиями: Вычислить площадь фигуры, ограниченной линиями:
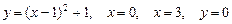 . .
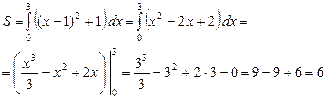
|
| 9.3.1(4) | Вычислить площадь фигуры, ограниченной линиями: 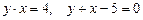 . .
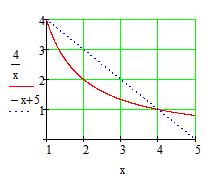 Найдем точки пересечения функций Найдем точки пересечения функций  : :
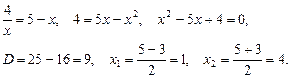 Т.о., площадь S искомой фигуры имеет вид:
Т.о., площадь S искомой фигуры имеет вид:
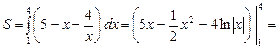
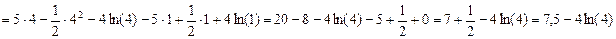
|
| 9.3.4(4) | Вычислить площадь фигуры, ограниченной линиями: 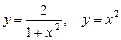 .
Найдем точки пересечения этих функций: .
Найдем точки пересечения этих функций:
 
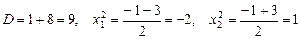 Нам подходит только случай
Нам подходит только случай  , поэтому , поэтому 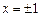 .
Т.о., площадь S искомой фигуры имеет вид: .
Т.о., площадь S искомой фигуры имеет вид:

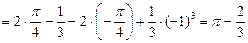 . .
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|