Итоговая контрольная работа по геометрии. 10 класс.

Итоговая контрольная работа по геометрии. 10 класс.

ВАРИАНТ 1.

1. а Дано: а (АВС),

М АВС – прямоугольный,

С= 90˚

В Доказать: МСВ -

А прямоугольный.

2. АВСDA₁B₁C₁D₁ – правильная призма. АВ = 6см, АА₁= 8см.

Найти угол между прямыми АА₁ и ВС; площадь полной поверхности призмы.

3. В правильной треугольной пирамиде сторона основания равна 2 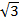см, а высота равна 2 см. Найти угол наклона бокового ребра к плоскости основания. Ответ запишите в градусах.

4. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120˚ между ними. Наибольшая из площадей боковых граней равна 56 см². Найти площадь полной поверхности призмы.

5. Дан прямоугольный треугольник АВС с гипотенузой АС=13 см и катетом ВС = 5 см. Отрезок SA = 12 см, - перпендикуляр к плоскости АВС. Найдите: а) длину суммы векторов СВ, SC и AS; б) угол между прямой SB и плоскостью АВС.

6. Постройте сечение куба АВСDA₁B₁C₁D₁, проходящего через вершину D и середины рёбер АА₁ и А₁В_1.

Итоговая контрольная работа по геометрии. 10 класс.

ВАРИАНТ 2.

1. М Дано: ABCD – ромб,

В С АС 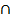ВD = О,

а (АВС).

Доказать: МО ВD.

OOOОО

А D

2. АВСDA₁B₁C₁D₁ – правильная призма. Площадь её полной поверхности равна 210 м², а площадь боковой поверхности 160 м². Найти сторону основания и высоту призмы.

3. В правильной четырёхугольной пирамиде со стороной основания 6 см и длиной бокового ребра 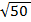см найти косинус угла наклона бокового ребра к плоскости основания и площадь боковой поверхности.

4. Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60˚. Меньшая из площадей диагональных сечений равна 130 см². Найти площадь полной поверхности параллелепипеда.

5. Дан прямоугольный треугольник АВС с гипотенузой АС=16 см и катетом ВС = 12 см. Отрезок SС = 20 см, - перпендикуляр к плоскости АВС. Найдите: а) длину суммы векторов CS, CB и BA; б) угол между прямой SA и плоскостью АВС.

6. Постройте сечение куба АВСDA₁B₁C₁D₁, проходящего через прямую АВ и середину ребра В₁С_1.