
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант № 26431623. Задание 1. Решение.. Задание 2. Решение.. Задание 3. Решение.. Задание 4. Решение.. Задание 5. Решение.. Задание 6. Решение.. Задание 7. Решение.. Задание 8. Решение.. Задание 9. Решение.. Задание 10. Решение.. Примечание.
Вариант № 26431623
ОГЭ14
1. Задание 1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | гостиная | кухня | ванная комната | кладовая комната |
| Цифры |
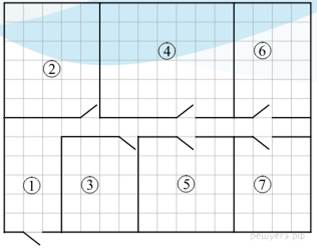
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.
Гостиная занимает наибольшую площадь в квартире, а слева от неё находится кухня. Прямо перед гостиной находится детская.
В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната.
В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м × 0,5 м.
В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
Решение.
Поскольку гостиная занимает наибольшую площадь в квартире, можно заключить, что она обозначена на схеме цифрой 4. Слева от гостиной находится кухня, следовательно, она обозначена цифрой 2. Ванная комната находится напротив санузла, значит, ванная обозначена на схеме цифрой 7. Кладовая комната расположена справа от коридора, следовательно, она обозначена цифрой 3.
Ответ: 4273.
2. Задание 2
Плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки. Площадь санузла равна 6 · 4 = 24 м2. Площадь ванной равна 4 · 5 = 20 м2. Теперь найдём, сколько упаковок плитки понадобилось: 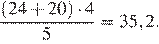 Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Ответ: 36.
3. Задание 3
Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь гостиной равна:
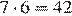 м2.
м2.
Ответ: 42.
4. Задание 4
Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой верхнего левого угла квартиры и нижнего правого угла квартиры по теореме Пифагора:
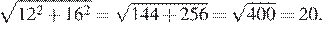
Ответ: 20.
5. Задание 5
Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о тарифах оплаты, и их стоимости даны в таблице.
| Оборудование и монтаж | Сред. потребл. мощность в час | Стоимость оплаты | |
| Однотарифный | 5100 руб. | 3,5 кВт · ч | 2 руб./(кВт · ч ) |
| Двухтарифный | 10 000 руб. | 3,5 кВт · ч | 2 руб./(кВт · ч) днём |
| 1 руб./(кВт · ч ) ночью (с 23:00 до 6:00) |
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна 10 000 − 5 100 = 4 900 руб. День использования электроэнергии с однотарифным счётчиком стоит 2 · 3,5 · 24 = 168 руб./(кВт · ч). День использования электроэнергии с двухтарифным счётчиком стоит 3,5 · 2 · 17 + 3,5 · 1 · 7 = 143,5 руб./(кВт · ч). Разница в стоимости составляет 168 − 143,5 = 24,5 руб./(кВт · ч). Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через 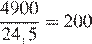 дней.
дней.
Ответ: 200.
6. Задание 6
Найдите значение выражения 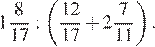
Решение.
Выполним действия в скобках, затем деление:
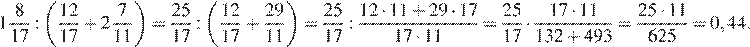
Ответ: 0,44.
7. Задание 7
На координатной прямой отмечено число а.
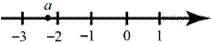
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) 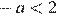
2) 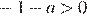
3) 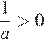
4) 
Решение.
Заметим, что 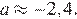 Проверим все варианты ответа:
Проверим все варианты ответа:
1) 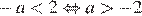 — неверно,
— неверно,
2) 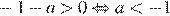 — верно,
— верно,
3)  — неверно,
— неверно,
4) 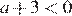 — неверно.
— неверно.
Правильный ответ указан под номером 2.
8. Задание 8
Найдите значение выражения 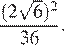
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 4
Решение.
Последовательно получаем:

Правильный ответ указан под номером 1.
9. Задание 9
Решите уравнение 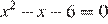 .
.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.
Тем самым, это числа −2 и 3.
Ответ: −23.
10. Задание 10
Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Решение.
Всего трехзначных чисел 900. На пять делится каждое пятое их них, то есть таких чисел 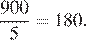 Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел:
Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел: 
Ответ: 0,2.
Примечание.
Количества чисел можно было не находить: искомая вероятность равна одной пятой потому, что пятая часть чисел делится на 5.
11. Задание 11
Найдите значение 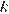 по графику функции
по графику функции 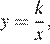 изображенному на рисунке.
изображенному на рисунке.
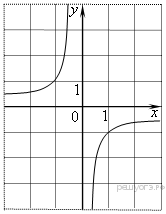
Решение.
Поскольку гипербола проходит через точку (−1; 1), имеем: 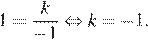
Ответ: −1.
12. Задание 12
Дана геометрическая прогрессия (bn), для которой b5 = −14, b8 = 112. Найдите знаменатель прогрессии.
Решение.
Член геометрической прогрессии с номером n вычисляется по формуле 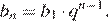 Зная, что b5 = −14 и b8 = 112, получаем систему уравнений. Решим систему, разделив второе уравнение на первое:
Зная, что b5 = −14 и b8 = 112, получаем систему уравнений. Решим систему, разделив второе уравнение на первое:

Ответ: −2.
13. Задание 13
Упростите выражение 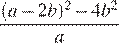 и найдите его значение при
и найдите его значение при 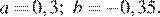
Решение.
Упростим выражение:
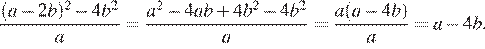
Найдем значение выражения при 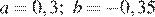 :
:

Ответ: 1,7.
14. Задание 14
Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Решение.
Подставим в формулу значение переменной 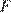 :
:
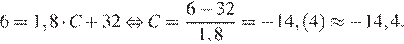
Ответ: −14,4.
15. Задание 15
Решите неравенство 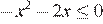 .
.
В ответе укажите номер правильного варианта.
1) 
2) 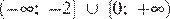
3) 
4) 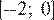
Решение.
Решим неравенство:
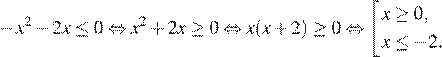
Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.
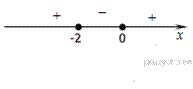
Правильный ответ указан под номером 2
16. Задание 16
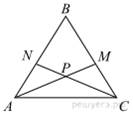
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите 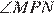 .
.
Решение.
В равностороннем треугольнике ABC все углы равны 60°. Биссектрисы CN и AM делят углы пополам, поэтому 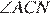 =
= 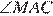 =
= 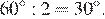 Сумма углов в треугольнике равна 180°, поэтому
Сумма углов в треугольнике равна 180°, поэтому 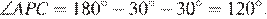 Вертикальные углы равны, следовательно,
Вертикальные углы равны, следовательно, 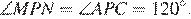
Ответ: 120.
17. Задание 17

На окружности с центром O отмечены точки A и B так, что 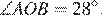 Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги 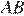 равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
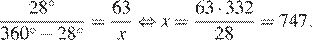
Ответ: 747.
18. Задание 18
Радиус круга равен 1. Найдите его площадь, деленную на π.
Решение.
Площадь круга равна:
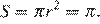
Ответ: 1.
---------------
В открытом банке ответ c числом π.
19. Задание 19
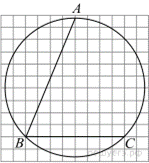
Найдите угол 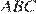 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.
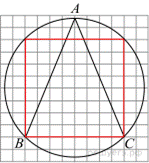
Проведём вспомогательное построение. Заметим, что дуга BC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги BC: 90°/2 = 45°. Треугольник 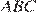 — равнобедренный, следовательно,:
— равнобедренный, следовательно,:

Ответ: 67,5.
20. Задание 20
Укажите номера верных утверждений.
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны.
2) Через любые три точки проходит не более одной прямой.
3) Сумма вертикальных углов равна 180°.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) Если при пересечении двух прямых третьей прямой соответственные углы равны, то эти две прямые параллельны. Утверждение 1 верно, в силу признака параллельности прямых.
2) Через любые три точки проходит не более одной прямой. Утверждение верно, через любые три точки либо нельзя провести прямую, если они не лежат на одной прямой, либо можно провести одну прямую, если они лежат на одной прямой.
3) Вертикальные углы равны по построению, при этом их сумма равна 180°, только если эти углы прямые, утверждение 3 неверно.
Ответ: 12.
21. Задание 21
Упростите выражение: 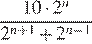 .
.
Решение.
Имеем:
 .
.
Ответ: 4.
22. Задание 22
Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение.
Пусть первый оператор может выполнить данную работу за  часов, а второй за
часов, а второй за  часов. За один час первый оператор выполняет
часов. За один час первый оператор выполняет  часть всей работы, а второй
часть всей работы, а второй  . Составим систему уравнений:
. Составим систему уравнений:
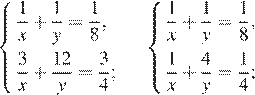
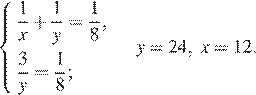
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.
23. Задание 23
Постройте график функции 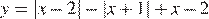 и найдите значения
и найдите значения 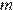 , при которых прямая
, при которых прямая  имеет с ним ровно две общие точки.
имеет с ним ровно две общие точки.
Решение.
Раскроем модули:
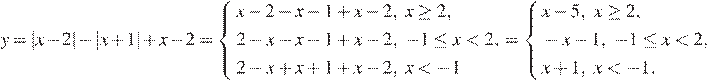
Получаем, что график функции совпадает с прямой 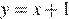 при
при  , совпадает с прямой
, совпадает с прямой 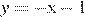 при
при 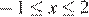 и совпадает с прямой
и совпадает с прямой 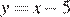 при
при 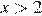 .
.
График изображен на рисунке. 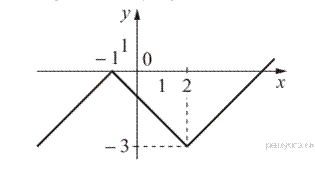
Прямая  имеет с графиком данной функции ровно две общие точки при
имеет с графиком данной функции ровно две общие точки при  или
или  .
.
Ответ: 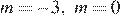 .
.
24. Задание 24
Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если ∠АВС = 20°.
Решение.
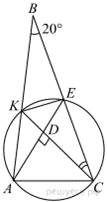
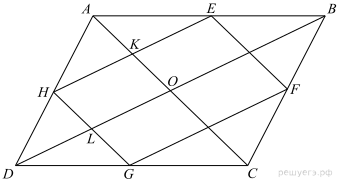
Углы АКС и АЕС равны, т. к. опираются на одну дугу окружности; следовательно, ∠ВКС = ∠ВЕА, как смежные с ними. Из четырёхугольника ВКDЕ: 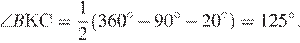 Из
Из 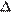 ВКС: ∠КСВ = 180° − 125° − 20° = 35°.
ВКС: ∠КСВ = 180° − 125° − 20° = 35°.
Ответ: 35°.
25. Задание 25
В окружности через середину O хорды AC проведена хорда BD так, что дуги AB и CD равны. Докажите, что O — середина хорды BD.
Решение.

Вписанные углы ADB, CBD , ACB и DAC опираются на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен AO:OC. Поскольку AO = OC , эти треугольники равны, следовательно, BO = OD.
26. Задание 26
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
Решение.
 Введём обозначения, как показано на рисунке. Поскольку
Введём обозначения, как показано на рисунке. Поскольку 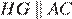 и
и 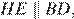 получаем, что HKOL — параллелограмм, следовательно, углы KHL и KOL равны. Рассмотрим треугольники ABC и EBF, угол EBF — общий, углы BEFи BAC равны как соответственные при параллельных прямых, углы BFE и BCA — аналогично, следовательно, треугольники ABC и BEF подобны по двум углам. Откуда
получаем, что HKOL — параллелограмм, следовательно, углы KHL и KOL равны. Рассмотрим треугольники ABC и EBF, угол EBF — общий, углы BEFи BAC равны как соответственные при параллельных прямых, углы BFE и BCA — аналогично, следовательно, треугольники ABC и BEF подобны по двум углам. Откуда  Аналогично подобны треугольники ABD и AEH, откуда
Аналогично подобны треугольники ABD и AEH, откуда  Пусть сторона ромба равна a, а длина короткой диагонали равна d. Сложим два полученных уравнения:
Пусть сторона ромба равна a, а длина короткой диагонали равна d. Сложим два полученных уравнения:
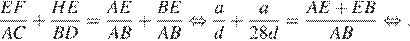

Площадь ромба можно найти как произведение сторон на синус угла между ними:  Площадь параллелограмма можно найти как половину произведения диагоналей на синус угла между ними:
Площадь параллелограмма можно найти как половину произведения диагоналей на синус угла между ними: 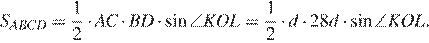 Найдём отношение площадей ромба и параллелограмма:
Найдём отношение площадей ромба и параллелограмма:

Ответ: 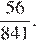
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|