
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №18. ПО «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ». на тему «Решение игр в смешанных стратегиях. Сведение игры к задаче линейного программирования».. Задача 1
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Гжельский государственный университет»(ГГУ)
Колледж ГГУ
Специальность 09.02.07 Информационные системы и программирование
Практическая работа №18
ПО «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»
на тему «Решение игр в смешанных стратегиях. Сведение игры к задаче линейного программирования».
ВЫПОЛНИЛА:
Студентка группы ИСП-О-18
Лобанов Марина Сегреевна
ПРОВЕРИЛА:
Шелепова Татьяна Сергеевна
Оценка ___________________
п. Электроизолятор
2020 г.
Цель работы:
1. Отработать и закрепить умения составлять для конечной парной антагонистической игры платежные матрицы для игроков по условиям игры.
2. Отработать и закрепить умения определять основные параметры матричной игры: верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии, чистую цену игры.
3. Отработать и закрепить умения сводить игру размера mxn заданную платежной матрицей к двойственным задачам линейного программирования.
4. Отработать и закрепить умение находить решение матричной игры mxn в смешанных стратегиях с помощью надстройки «Поиск решения» MS Excel.
Задача 1
Каждый из игроков А и В записывает одно из чисел N1,N2,N3 или N4, затем они одновременно показывают написанное. Если оба числа оказались одинаковой четности, то игрок А выигрывает столько очков, какова сумма этих чисел, если разной четности – выигрывает игрок В. Составить платежную матрицу, найти нижнюю и верхнюю чистые цены игры, максиминную и минимаксную стратегии игроков. Указать наличие седловой точки (если она есть).
| №Варианта | N1 | N2 | N3 | N4 |
Решение
1. Составим платежную матрицу
Пусть A1 – стратегия первого игрока, он записывает число 3, А2 – стратегия первого игрока, он записывает число 8, A3 – стратегия первого игрока, он записывает число 5, А4 – стратегия первого игрока, он записывает число 9.
В1 – стратегия второго игрока, он записывает число 3, В2 – стратегия второго игрока, он записывает число 8, В3 – стратегия второго игрока, он записывает число 5, В4 – стратегия второго игрока, он записывает число 9.
Если 1-й игрок применит первую стратегию и второй игрок тоже (оба запишут 3), то оба числа оказываются одинаковой четности, игрок А выигрывает 3 + 3 = 6.
Если 1-й игрок применит первую стратегию (напишет 3), а второй игрок использует вторую стратегию (напишет 8), то оба числа оказываются разной четности, игрок В выигрывает 3+ 8 = 11.
Если 1-й игрок применит первую стратегию (напишет 3), а второй игрок использует третью стратегию (напишет 5), то оба числа оказываются одинаковой четности, игрок А выигрывает 3 + 5 = 8.
Если 1-й игрок применит первую стратегию (напишет 3), а второй игрок использует четвертую стратегию (напишет 9), то оба числа оказываются разной четности, игрок А выигрывает 3 + 9 = 12.
Если 1-й игрок применит вторую стратегию (напишет 8), а второй игрок использует первую стратегию (напишет 3), то оба числа оказываются разной четности, игрок В выигрывает 8 + 3 = 11.
Если 1-й игрок применит вторую стратегию (напишет 8), а второй игрок использует вторую стратегию (напишет 8), то оба числа оказываются одинаковой четности, игрок А выигрывает 8 + 8 = 16.
Если 1-й игрок применит вторую стратегию (напишет 8), а второй игрок использует третью стратегию (напишет 5), то оба числа оказываются разной четности, игрок В выигрывает 8 + 5 = 13.
Если 1-й игрок применит вторую стратегию (напишет 8), а второй игрок использует четвертую стратегию (напишет 7), то оба числа оказываются одинаковой четности, игрок В выигрывает 8 + 9 = 17.
Если 1-й игрок применит третью стратегию (напишет 5), а второй игрок использует первую стратегию (напишет 3), то оба числа оказываются одинаковой четности, игрок А выигрывает 5+3=8.
Если 1-й игрок применит третью стратегию (напишет 5), а второй игрок использует вторую стратегию (напишет 8), то оба числа оказываются разной четности, игрок В выигрывает 5+8=13.
Если 1-й игрок применит третью стратегию (напишет 5), а второй игрок использует третью стратегию (напишет 5), то оба числа оказываются одинаковой четности, игрок А выигрывает 5+5=10.
Если 1-й игрок применит третью стратегию (напишет 5), а второй игрок использует четвертую стратегию (напишет 9), то оба числа оказываются разной четности, игрок А выигрывает 5+9=14.
Если 1-й игрок применит четвертую стратегию (напишет 9), а второй игрок использует первую стратегию (напишет 3), то оба числа оказываются разной четности, игрок А выигрывает 9+3=12.
Если 1-й игрок применит четвертую стратегию (напишет 9), а второй игрок использует вторую стратегию (напишет 8), то оба числа оказываются одинаковой четности, игрок В выигрывает 9+8=17.
Если 1-й игрок применит четвертую стратегию (напишет 9), а второй игрок использует третью стратегию (напишет 5), то оба числа оказываются разной четности, игрок А выигрывает 9+5=14.
Если 1-й игрок применит четвертую стратегию (напишет 9), а второй игрок использует четвертую стратегию (напишет 9), то оба числа оказываются одинаковой четности, игрок А выигрывает 9 + 9 = 18.
Таким образом, получим матрицу выигрышей игрока А:
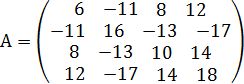
Величина 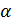 - гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия, обеспечивающая получение выигрыша α, называется максиминной. Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше α.
- гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия, обеспечивающая получение выигрыша α, называется максиминной. Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше α.
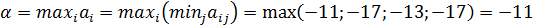
Величина 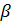 - гарантированный проигрыш игрока В называется верхней ценой игры. Стратегия, обеспечивающая получение проигрыша β, называется минимаксной. Если второй игрок будет придерживаться своей минимаксной стратегии, то у него есть гарантия, что он в любом случае проиграет не больше
- гарантированный проигрыш игрока В называется верхней ценой игры. Стратегия, обеспечивающая получение проигрыша β, называется минимаксной. Если второй игрок будет придерживаться своей минимаксной стратегии, то у него есть гарантия, что он в любом случае проиграет не больше 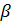 .
.
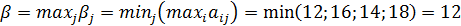
Поскольку 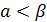 , то платежная матрица не имеет седловую точку, т.е. она решается в смешанных стратегиях.
, то платежная матрица не имеет седловую точку, т.е. она решается в смешанных стратегиях.
Цена игры находится в пределах:
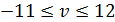
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|