
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сведения из теории:. Пример.
Сведения из теории:
Случайные величины (дискретные и непрерывные) характеризуются своим законом распределения.
Простейшей, но очень важной характеристикой является математическое ожидание.
Пусть, например, X - дискретная случайная величина распределена по закону:
| X | х1 | х2 | … | хп |
| P | p1 | p2 | … | рп |
Тогда ее математическое ожидание М(Х) определяется равенством
М (Х) = х1 p1+ х2 p2+…+ хп рп.
Пусть, например, испытание состоит в бросании игрального кубика. Поскольку выпадение каждой грани равновозможно, Pi=1/6. Следовательно, математическое ожидание числа выпавших очков равно
М(Х) = 1/6(1 + 2 + 3 + 4 + 5 + 6) = 21/6 = 3,5.
Число, близкое к этому, получится, если реально бросать кубик много раз и подсчитать сумму очков, деленную на число бросков.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D{X) = М[Х- М(Х)]2.
Так же дисперсию можно вычислить и по формуле:
D{X) = М(Х2)- [М(Х)]2,
т. е. как разность математического ожидания квадрата значений случайной величины и квадрата её математического ожидания.
Многие случайные величины, встречающиеся на практике, имеют размерность. Поэтому вводится еще одна характеристика, называемая средним квадратическим отклонением, обозначается: 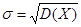 . ее размерность совпадает с размерностью случайной величины.
. ее размерность совпадает с размерностью случайной величины.
Пример.
Пусть Х – число очков, выпадающих при одном бросании игральной кости. Найти дисперсию случайной величины Х.
Решение:
случайная величина Х – число очков принимает значения 1, 2, 3, 4, 5, 6. Составим закон её распределения:
| Xi | ||||||
| Pi | 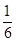
| 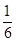
| 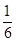
| 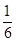
| 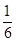
| 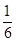
|
Тогда её математическое ожидание:
М(Х)= 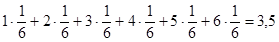 .
.
Найдем отклонения для х1, х2, …, х6:
х10=1-3,5; х20=2-3,5; х30=3-3,5; х40=4-3,5; х50=5-3,5; х60=6-3,5.
Вычислим дисперсию:
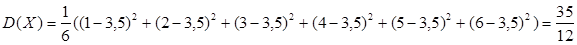 .
.
Вычислим среднее квадратичное отклонение 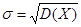 ;
;
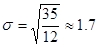
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|