Урок 143-144 13.05.2020 МОС-19-1

Урок 143-144 13.05.2020 МОС-19-1

Тема: Усеченная пирамида

Цель урока: ознакомить студентов с понятием усеченная пирамида, её элементами и формулами для вычисления площадей боковой и полной поверхностей;

Вопросы:

1. Что называется пирамидой? Правильной пирамидой?

2. Что называется площадью боковой поверхности пирамиды?

3. Что называется площадью полной поверхности пирамиды?

4. Что называется трапецией? Равнобедренной? Прямоугольной?

5. Как найти площадь трапеции?

6. Устно решите задачи (а, б)

Дано: ABCD - трапеция; ∠BAD = 45°. ВС = 6 см, AD = 8 см.

Найти: S - ?

Решение:

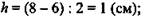
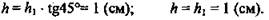
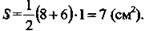
(Ответ: S = 7 см²)

Задача 2 (устно)

Дано: ABCD - трапеция. АВСК - квадрат. ВС = 4√3 см. ∠CDK = 30°.

Найти: AD - ?

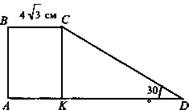
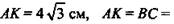
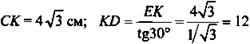
Решение: 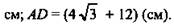(Ответ: )

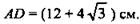Объяснение темы

Задание

Изобразить произвольную пирамиду P_A₁_A_{2 ... А}_n

Возьмем произвольную пирамиду Р_{А1А2 ... А}_n и проведем секущую плоскость β, параллельно плоскости α основания пирамиды и пересекающую боковые ребра в точках В₁,В₂, ... В_n. Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники А₁А₂, ... А_n и В₁В₂, ... В_n (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n-четырехугольников А₁А₂В₂В₁, А₂А₃В₃В₂, ... А_nА₁В₁В_n (боковые грани), называется усеченной пирамидой.

Отрезки A₁B₁, А₂В₂, ... А_nВ_n называются боковыми ребрами усеченной пирамиды. Усеченную пирамиду с основаниями А1А2...Аn и В1В2...Вn обозначают так: А1А2...Аn В1В2...Вn. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды».

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды - правильные многоугольники, а боковые грани - равнобедренные трапеции. Высоты этих трапеций называются апофемами. Как найти сумму площадей ее боковых граней?

Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.

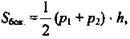где р₁ и р₂ - периметры оснований, h - апофема.

Теорема

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему

Решение задач

Дано:

MABCD - правильная пирамида, А1В1С1 || АВС, МО1 : O1O = 1: 2, NK - апофема, NK = 4 дм, Syc.пиp. = 186 дм2

Найти: ОО1 - ?

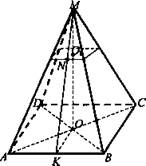
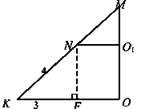
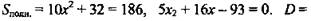
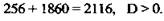
Решение: Рассмотрите ΔМКО. Так как NO1 || KO, то МО1 : МО = O1N : OK, значит, стороны В1С1 : ВС = МО1 : МО. В1С1 = 1 : 3. Пусть В1С1 = х, ВС = 3х. Имеем 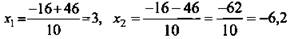(не удовлетворяет условию задачи); В1С1 = 3 (см), NО = 1,5 (см); ВС = 9 (см), ОК = 4,5 (см); KF = OK – NO1 = 3. Из ΔKNF по теореме Пифагора 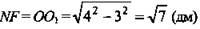(Ответ: √7 дм.)

№ 2 Дано: АВСА1В1С1 — усеченная пирамида. АВ = ВС = АС = 4 см; A1B1 = B1C1 = A1C1 = 2 см; АА1 = 2 см.

Найти: МК- ? A\F\ - ?

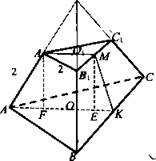
Решение: Пусть О и О1 - центры оснований пирамиды.

1) Из ΔАВС имеем: АВ = R√3, R = АО.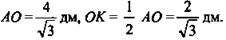

2) Из ΔА1B1C1 находим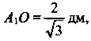

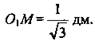
3) EK = ОK - OE, ОЕ = O1М, отсюда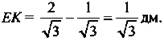

4) Из ΔAA1F имеем:

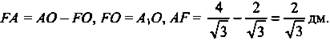
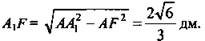
5) Из ΔМЕК имеем: 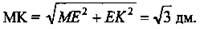(Ответ: )

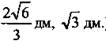Домашнее задание

Тест

Оценка ставится в зависимости от суммы баллов, набранных учеником, причем правильный ответ оценивается в 2 балла, неправильный - в 1, ответ «не знаю» оценивается в 0 баллов.

Примерная шкала оценок.

Оценки: 3 4 5

Баллы: 3-7 8-10 12

Вариант I

1. Из данных утверждений выберите верное: а) все ребра правильной пирамиды равны; б) площадь поверхности пирамиды равна половине произведения периметра основания на апофему; в) боковые грани усеченной пирамиды - трапеции; г) утверждения a-в не верны.

2. Найдите площадь боковой поверхности пирамиды, все грани которой наклонены к основанию под углом 60°, а в основании лежит прямоугольный треугольник с катетами 3 см и 6 см.

а) 9 см2, б) 10 см2, в) 12 см2, г) другой ответ.

3. В правильной четырехугольной пирамиде сторона основания равна 5 см, а плоский угол при вершине пирамиды 60°. Найдите боковое ребро пирамиды.

а) 6 см, б) 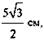в) 5 см, г) д) другой ответ.

4. В основании пирамиды SABC лежит равнобедренный треугольник ABC, в котором ВС = 12 см, а АВ = АС = 10 см. Найдите площадь сечения ASM, если оно перпендикулярно плоскости основания, а все боковые ребра пирамиды равны 10 см.

а) 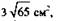б) 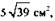в) 31 см2, г) другой ответ.

5. Боковые ребра пирамиды SABC равны между собой. SD - высота пирамиды. Точка D лежит внутри ΔABC. ТреугольникABC:

а) прямоугольный;

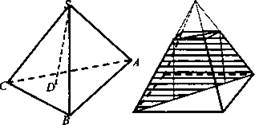б) остроугольный;

в) тупоугольный;

г) недостаточно данных.

6. Найдите площадь диагонального сечения правильной усеченное четырехугольной пирамиды, если ее высота равна √2 см, а стороны основания 1 см и 4 см.

а) 10 см2, б) 2,5 см2, в) 5 см2, г) другой ответ.