
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Самостоятельная работа
08.05.2020. Урок геометрии
Урок 60. Свойство описанного четырехугольника
| Создать условия для выведения свойства описанного четырехугольника и совершенствовать навыки решения задач с использованием свойства описанного четырехугольника | ||||||
| Задания для индивидуальной работы | ||||||
| Тест 1. Центр вписанной в треугольник окружности совпадает с точкой пересечения его... а) медиан; б) биссектрис; в) серединных перпендикуляров. 2. Центр вписанной в треугольник окружности равноудален от... а) сторон; б) углов; в) вершин треугольника. 3. Центр вписанной в треугольник окружности является точкой пересечения его медиан. Этот треугольник... а) прямоугольный; б) равнобедренный; в) равносторонний. 4. Окружность называется вписанной в многоугольник, если... а) все его стороны касаются окружности; б) все его вершины лежат на окружности; в) все его стороны имеют общие точки с окружностью. Мне ответы. | ||||||
Решить задачи.
| ||||||
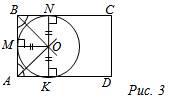
1. Заметим, что не во всякий четырехугольник можно вписать окружность, на пример:
а) прямоугольника (рис. 3); б) параллелограмма (рис. 4).
| ||||||
Посмотрите устно решение № 697.
Доказательство: SАВСD = SАВO + SBOC + SCOD + SAOD SАВСD = | ||||||
Самостоятельная работа
1. В равносторонний треугольник вписана окружность радиусом 4 см. Найдите сторону треугольника.
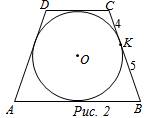
2. Четырехугольник ABCD описан около окружности. Найдите стороны АВ и CD, если ВС = 6 см, AD = 9 см, АВ в два раза больше, чем CD.


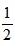 PАВСD · R.
PАВСD · R.