Тема: «Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка

Тема: «Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка"

Задание 1. Изучите теоретический материал, сделайте конспект.

Теоретический материал

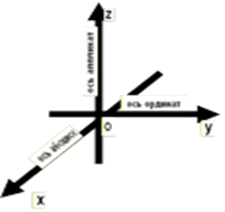
Определение. Прямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных координатных прямых с общим началом координат.

Общее начало координат обозначается буквой O.

Ох – ось абсцисс, Оу – ось ординат, Оz – ось аппликат

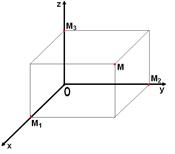
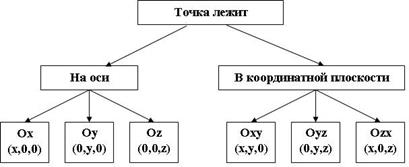
Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz, Оzх.

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты.

М (х,у,z), где х – абсцисса, у – ордината, z - аппликата.

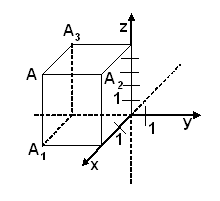
Зависимость положения точки в пространстве и координат этой тточки

Расстояние между точками

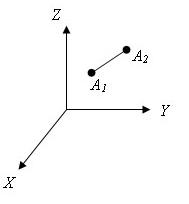
Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂)

Тогда расстояние между точками A₁ и A₂ вычисляется так:

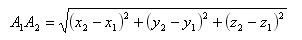
Координаты середины отрезка в пространстве

Есть две произвольные точки A₁(x₁;y₁;z₁) и A₂(x₂;y₂;z₂). Тогда серединой отрезка A₁A₂ будет точка С с координатами x, y, z, где

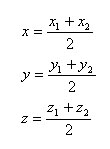
Задание 2. Решите задачи, используя формулы из теоретического материала

1) Найдите координаты ортогональных проекций точек A(1, 3, 4) и B(5, -6, 2) на: а) плоскость Oxy; б) плоскость Oyz; в) ось Ox; г) ось Oz.

2) На каком расстоянии находится точка A(1, -2, 3) от координатной плоскости: а) Oxy; б) Oxz; в) Oyz?

3)Найдите координаты середины отрезка: а) AB, если A(1, 2, 3) и B(-1, 0, 1); б) CD, если C(3, 3, 0) и D(3, -1, 2). (Ответ: а) (1, 1, 2); б) (3, 1, 1).)